题目内容
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD= ![]() ∠BAC=60°,于是
∠BAC=60°,于是 ![]() =
= ![]() =
= ![]() ; 迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.
; 迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.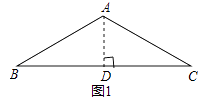
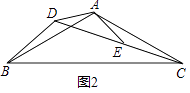
(1)①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;
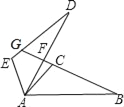
(2)拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF. 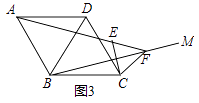
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.
【答案】
(1)解:①证明:如图②
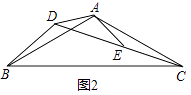
∵∠BAC=∠ADE=120°,
∴∠DAB=∠CAE,
在△DAE和△EAC中,
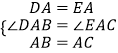 ,
,
∴△DAB≌△EAC,
②解:结论:CD= ![]() AD+BD.
AD+BD.
理由:如图2﹣1中,作AH⊥CD于H.
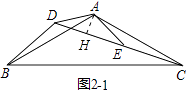
∵△DAB≌△EAC,
∴BD=CE,
在Rt△ADH中,DH=ADcos30°= ![]() AD,
AD,
∵AD=AE,AH⊥DE,
∴DH=HE,
∵CD=DE+EC=2DH+BD= ![]() AD+BD
AD+BD
(2)解::①证明:如图3中,作BH⊥AE于H,连接BE.

∵四边形ABCD是菱形,∠ABC=120°,
∴△ABD,△BDC是等边三角形,
∴BA=BD=BC,
∵E、C关于BM对称,
∴BC=BE=BD=BA,FE=FC,
∴A、D、E、C四点共圆,
∴∠ADC=∠AEC=120°,
∴∠FEC=60°,
∴△EFC是等边三角形,
②解:∵AE=5,EC=EF=2,
∴AH=HE=2.5,FH=4.5,
在Rt△BHF中,∵∠BHF=30°,
∴ ![]() =cos30°,
=cos30°,
∴BF= ![]() =3
=3 ![]()
【解析】迁移应用:①如图②中,只要证明∠DAB=∠CAE,即可根据SAS解决问题;②结论:CD= ![]() AD+BD.由△DAB≌△EAC,可知BD=CE,在Rt△ADH中,DH=ADcos30°=
AD+BD.由△DAB≌△EAC,可知BD=CE,在Rt△ADH中,DH=ADcos30°= ![]() AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=
AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD= ![]() AD+BD,即可解决问题; 拓展延伸:①如图3中,作BH⊥AE于H,连接BE.由BC=BE=BD=BA,FE=FC,推出A、D、E、C四点共圆,推出∠ADC=∠AEC=120°,推出∠FEC=60°,推出△EFC是等边三角形;
AD+BD,即可解决问题; 拓展延伸:①如图3中,作BH⊥AE于H,连接BE.由BC=BE=BD=BA,FE=FC,推出A、D、E、C四点共圆,推出∠ADC=∠AEC=120°,推出∠FEC=60°,推出△EFC是等边三角形;
②由AE=5,EC=EF=2,推出AH=HE=2.5,FH=4.5,在Rt△BHF中,由∠BHF=30°,可得 ![]() =cos30°,由此即可解决问题.
=cos30°,由此即可解决问题.