题目内容
设三角形ABC中BC边的长为x(cm),BC上的高AD为y(cm),三角形的面积是常数.已知y关于x的函数图象过点(3,4).
(1)求y关于x的函数解析式和三角形的面积;
(2)画出函数图象,并利用图象,求当2<x<8时y的取值范围.
(1)求y关于x的函数解析式和三角形的面积;
(2)画出函数图象,并利用图象,求当2<x<8时y的取值范围.
分析:(1)利用三角形面积公式以及y关于x的函数图象过点(3,4)得出函数解析式以及三角形的面积即可;
(2)利用函数解析式画出图象,再利用2<x<8求出对应y的值即可.
(2)利用函数解析式画出图象,再利用2<x<8求出对应y的值即可.
解答: 解:(1)由题意,S△ABC=
解:(1)由题意,S△ABC=
xy,
把点(3,4)代入,
得S△ABC=
xy=
×3×4=6,
∴y关于x的函数解析式是y=
,
△ABC的面积是6厘米2;
(2)如图所示:当x=2时,y=6;当x=8时,y=1.5,
由函数y=
图象的性质得,在第一象限y随x的增大而减小,
∴当2<x<8时,y的取值范围是1.5<y<6.
 解:(1)由题意,S△ABC=
解:(1)由题意,S△ABC=| 1 |
| 2 |
把点(3,4)代入,
得S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴y关于x的函数解析式是y=
| 12 |
| x |
△ABC的面积是6厘米2;
(2)如图所示:当x=2时,y=6;当x=8时,y=1.5,
由函数y=
| 12 |
| x |
∴当2<x<8时,y的取值范围是1.5<y<6.
点评:此题主要考查了反比例函数的应用以及函数与三角形的混合问题,应用数形结合的方法进行求解是解题关键.

练习册系列答案
相关题目
 B点,同时点Q以2米/分的速度从点B移动到C点(当一个点到达后全部停止移动).
B点,同时点Q以2米/分的速度从点B移动到C点(当一个点到达后全部停止移动).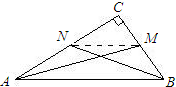 求证:在直角三角形中两条直角边上的中线的平方和的4倍等于斜边平方的5倍.如图所示.设直角三角形ABC中,∠C=90°,AM,BN分别是BC,AC边上的中线,且AM2+BN2=AB2+MN2.
求证:在直角三角形中两条直角边上的中线的平方和的4倍等于斜边平方的5倍.如图所示.设直角三角形ABC中,∠C=90°,AM,BN分别是BC,AC边上的中线,且AM2+BN2=AB2+MN2. 在直角三角形ABC中,BC=6,AC=8,点D在线段AC上从C向A运动.若设CD=x,△ABD的面积为y.
在直角三角形ABC中,BC=6,AC=8,点D在线段AC上从C向A运动.若设CD=x,△ABD的面积为y.