Question

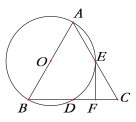
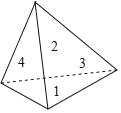
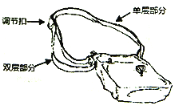
【题目】如图1所示的是午休时老师们所用的一种折叠椅，现将躺椅以如图2所示的方式倾斜放置，AM与地面ME成45°角，AB∥ME，椅背BC与水平线成30°角，其中AM＝50厘米，BC＝72厘米，BP是躺椅的伸缩支架，且30°≤BPM≤90°．(结果精确到1厘米；参考数据≈1.4，≈ 1.7，≈ 2.2)

(1)求此时点C与地面的距离．

(2)在(1)的条件下，求伸缩支架BP可达到的最大值．

Answer 1

【答案】(1)此时点C与地面的距离是71厘米；(2)伸缩支架BP可达到的最大值是70厘米．

【解析】

（1）根据题意和图象，利用锐角三角函数可以解答本题；

（2）根据（1）中的条件和图形，可以求得伸缩支架BP可达到的最大值．

解：(1)∵AM与地面ME成45°角，AB∥ME，椅背BC与水平线成30°角，其中AM＝50厘米，BC＝72厘米，

∴点A到地面的距离为：AMsins45°＝50×＝25(厘米)，

CD＝BCsin30°＝72×＝36(厘米)，

∴点C与地面的距离是：25+36≈71(厘米)，

即此时点C与地面的距离是71厘米；

(2)∵AB∥ME，

∴点B到ME的距离是25厘米，

∴BP＝，

∵30°≤BPM≤90°，

∴当∠MPM＝30°时，

BP取得最大值，此时BP＝＝50≈70(厘米)，

即伸缩支架BP可达到的最大值是70厘米．