题目内容
 探索规律:
探索规律:观察下面由※组成的图案和算式,解答问题:
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请猜想1+3+5+7+9+…+29=
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n+1)=
(3)请用上述规律计算:41+43+45+…+77+79.
分析:(1)根据1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,可知,
=2;
=3;
=4;
=5;则得1+3+5+7+9+…+29的值.
(2)由(1)可猜到其和为该组数据平均数的平方;
(3)将41+43+45+…+77+79看作1+3+5+…+39+41+43+45+…+77+79与1+3+5+…+39的差.
| 1+3 |
| 2 |
| 1+5 |
| 2 |
| 1+7 |
| 2 |
| 1+9 |
| 2 |
(2)由(1)可猜到其和为该组数据平均数的平方;
(3)将41+43+45+…+77+79看作1+3+5+…+39+41+43+45+…+77+79与1+3+5+…+39的差.
解答:解:(1)有规律可知,1+3+5+7+9+…+29=(
)2=152;
(2)由(1)可知1+3+5+7+9+…+(2n-1)+(2n+1)=[
]2;
(3)41+43+45+…+77+79=(1+3+5+…+39+41+43+45+…+77+79)-(1+3+5+…+39)=(
)2-(
)2=1600-400=1200.
| 1+29 |
| 2 |
(2)由(1)可知1+3+5+7+9+…+(2n-1)+(2n+1)=[
| 1+(2n+1) |
| 2 |
(3)41+43+45+…+77+79=(1+3+5+…+39+41+43+45+…+77+79)-(1+3+5+…+39)=(
| 1+79 |
| 2 |
| 1+39 |
| 2 |
点评:此题考查了数字的变化规律,善于观察与积累是解答此类问题的基本思想.

练习册系列答案
相关题目

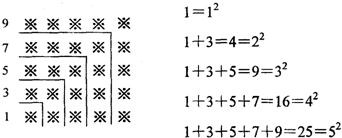

 32、探索规律:观察下面由※组成的图案和算式,解答问题:
32、探索规律:观察下面由※组成的图案和算式,解答问题: 探索规律:观察下面由※组成的图案和算式,解答问题:
探索规律:观察下面由※组成的图案和算式,解答问题: 探索规律:观察下面由※组成的图案和算式,
探索规律:观察下面由※组成的图案和算式,