Question

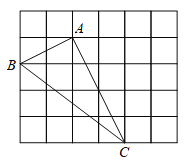
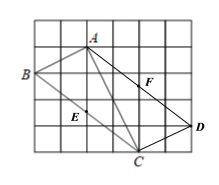
【题目】如图，在由边长为1的小正方形组成的网格中，的三个顶点均在格点上，请解答：

（1）判断的形状，并说明理由；

（2）在网格图中画出AD//BC，且AD=BC；

（3）连接CD，若E为BC中点，F为AD中点，四边形AECF是什么特殊的四边形？请说明理由.

Answer 1

【答案】（1）是直角三角形，理由见解析；（2）图见解析；（3）四边形是菱形，理由见解析．

【解析】

（1）先结合网格特点，利用勾股定理求出三边长，再根据勾股定理的逆定理即可得；

（2）先利用平移的性质得到点D，再连接AD即可；

（3）先根据线段中点的定义、等量代换可得，再根据平行四边形的判定可得四边形AECF是平行四边形，然后根据直角三角形的性质可得，最后根据菱形的判定、正方形的判定即可得．

（1）是直角三角形，理由如下：

，，

即

是直角三角形；

（2）由平移的性质可知，先将点B向下平移3个单位，再向右平移4个单位可得点C

同样，先将点A向下平移3个单位，再向右平移4个单位可得点D，然后连接AD

则有，且，作图结果如下所示：

（3）四边形是菱形，理由如下：

为中点，为中点

，

，即

四边形是平行四边形

又为中点，是的斜边

平行四边形是菱形

不是等腰直角三角形

与BC不垂直，即

菱形不是正方形

综上，四边形是菱形．