Question

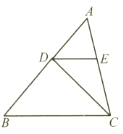
【题目】如图，在△ABC 中，AB=4，D 是 AB 上的一点（不与点 A、B 重合），DE∥BC，交AC 于点 E.设△ABC 的面积为 S，△DEC 的面积为 S'.

（1）当D是AB中点时，求的值；
（2）设AD=x，=y，求y与x的函数表达式，并写出自变量x的取值范围；
（3）根据y的范围，求S-4S′的最小值．

Answer 1

【答案】（1）答案见解析（2）答案见解析（3）答案见解析.

【解析】

（1）先求出△ADE和△CDE的面积相等，再根据平行线得出△ADE∽△ABC，推出比值关系，把AB=2AD代入求出即可（2）求出和,联立求出关系式即可（3）把函数解析式写成顶点式即可.

解：（1）∵D为AB中点，
∴AB=2AD，
∵DE∥BC，
∴AE=EC，
∵△ADE的边AE上的高和△CED的边CE上的高相等，

∵DE∥BC

（2）

①

∵△ADE的边AE上的高和△CED的边CE上的高相等

②

① 得：

x的取值范围是

（3）由（2）知x的取值范围是

的最小值为0.