题目内容
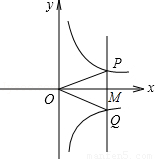
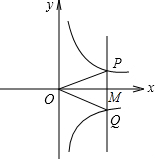 如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数y=
如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数y=| k1 |
| x |
| k2 |
| x |
(1)∠POQ不可能等于90°;
(2)
| PM |
| QM |
| k1 |
| k2 |
(3)这两个函数的图象一定关于x轴对称;
(4)△POQ的面积是
| 1 |
| 2 |
其中正确的有
(4)
(4)
(填写序号)分析:根据反比例函数k的几何意义,及反比例函数图象上点的坐标特征,分别进行各选项进行判断即可,注意用点的坐标表示线段长度时,一定要注意正负.
解答:解:(1)∵P点坐标不知道,当PM=MQ时,并且PM=OM,∠POQ等于90°,故此项错误;
(2)根据图形可得:k1>0,k2<0,设点P、Q的横坐标为a,则PM=
,MQ=
,故
=|
|,故此项错误;
(3)根据k1,k2的值不确定,得出这两个函数的图象不一定关于x轴对称,故此项错误;
(4)∵|k1|=PM•MO,|k2|=MQ•MO,△POQ的面积=
MO•PQ=
MO(PM+MQ)=
MO•PM+
MO•MQ,
∴△POQ的面积是
(|k1|+|k2|),故此项正确.
故答案为:(4).
(2)根据图形可得:k1>0,k2<0,设点P、Q的横坐标为a,则PM=
| k1 |
| a |
| |k2| |
| a |
| PM |
| QM |
| k1 |
| k2 |
(3)根据k1,k2的值不确定,得出这两个函数的图象不一定关于x轴对称,故此项错误;
(4)∵|k1|=PM•MO,|k2|=MQ•MO,△POQ的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴△POQ的面积是
| 1 |
| 2 |
故答案为:(4).
点评:此题主要考查了反比例函数的综合应用,根据反比例函数的性质得出|k1|=PM•MO,|k2|=MQ•MO是解题关键.

练习册系列答案
相关题目
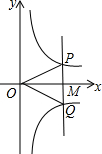 如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数
如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数 和
和 的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )