题目内容
已知:⊙O的半径OA=1,弦AB、AC的长分别为
,
,求∠BAC的度数.
| 2 |
| 3 |
分析:根据题意画出图形,作出辅助线,由于AC与AB在圆心的同侧还是异侧不能确定,故应分两种情况进行讨论.
解答: 解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,
∴AE=
AC=
,AD=
AB=
,
∴sin∠AOE=
=
=
,sin∠AOD=
=
,
∴∠AOE=60°,∠AOD=45°,
∴∠BAO=45°,∠CAO=90°-60°=30°,
∴∠BAC=45°+30°=75°,或∠BAC′=45°-30°=15°.
∴∠BAC=15°或75°.
 解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.∵OE⊥AC,OD⊥AB,
∴AE=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴sin∠AOE=
| AE |
| AO |
| ||||
| 1 |
| ||
| 2 |
| AD |
| OA |
| ||
| 2 |
∴∠AOE=60°,∠AOD=45°,
∴∠BAO=45°,∠CAO=90°-60°=30°,
∴∠BAC=45°+30°=75°,或∠BAC′=45°-30°=15°.
∴∠BAC=15°或75°.
点评:本题考查的是垂径定理及直角三角形的性质,解答此题时进行分类讨论,不要漏解.

练习册系列答案
相关题目
 如图,已知圆O的半径OA=2,C为半径OB的中点,若∠AOB=90°,则图中阴影部分的面积为
如图,已知圆O的半径OA=2,C为半径OB的中点,若∠AOB=90°,则图中阴影部分的面积为
 如图,已知大圆的半径OA=6cm,且AB⊥CD,则图中阴影部分的面积是
如图,已知大圆的半径OA=6cm,且AB⊥CD,则图中阴影部分的面积是

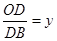 ,求y与x的函数关系式并写出自变量x 的取值范围。
,求y与x的函数关系式并写出自变量x 的取值范围。