题目内容
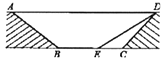
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面![]() 与通道
与通道![]() 平行),通道水平宽度
平行),通道水平宽度![]() 为8米,
为8米, ![]() ,通道斜面
,通道斜面![]() 的长为6米,通道斜面
的长为6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的长为 米;
的长为 米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面![]() 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面![]() 的坡角为30°,求此时
的坡角为30°,求此时![]() 的长.(结果保留根号)
的长.(结果保留根号)
【答案】(1)7.4米;(2)(8+3![]() -3
-3![]() )米
)米
【解析】试题分析: (1)过点A作AN⊥CB于点N,过点D作DM⊥BC于点M,根据已知得出DM=CM=![]() CD=3
CD=3![]() ,则AN=DM=3
,则AN=DM=3![]() ,再解Rt△ANB,由通道斜面AB的坡度i=1:
,再解Rt△ANB,由通道斜面AB的坡度i=1: ![]() ,得出BN=
,得出BN=![]() AN=6,然后根据勾股定理求出AB;
AN=6,然后根据勾股定理求出AB;
(2)先解Rt△MED,求出EM=![]() DM=3
DM=3![]() ,得出EC=EM-CM=3
,得出EC=EM-CM=3![]() -3
-3![]() ,再根据BE=BC-EC即可求解.
,再根据BE=BC-EC即可求解.
试题解析:(1)过点A作AN⊥CB于点N,过点D作DM⊥BC于点M,

∵∠BCD=135°,
∴∠DCM=45°.
∵在Rt△CMD中,∠CMD=90°,CD=6,
∴DM=CM=![]() CD=3
CD=3![]() ,
,
∴AN=DM=3![]() ,
,
∵通道斜面AB的坡度i=1: ![]() ,
,
∴tan∠ABN=![]() ,
,
∴BN=![]() AN=6,
AN=6,
∴AB=![]() =3
=3![]() ≈7.4.
≈7.4.
即通道斜面AB的长约为7.4米;
(2)∵在Rt△MED中,∠EMD=90°,∠DEM=30°,DM=3![]() ,
,
∴EM=![]() DM=3
DM=3![]() ,
,
∴EC=EM-CM=3![]() -3
-3![]() ,
,
∴BE=BC-EC=8-(3![]() -3
-3![]() )=(8+3
)=(8+3![]() -3
-3![]() )米
)米

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目