题目内容
有一列数，记为a1，a2，…an，我们记其前n项和为Sn=a1+a2+…．+an，定义Tn=| S1+S2+…+Sn | n |
分析：根据“奥运和”的定义Tn=
分析可得：现如果有99个数a1+a2+…+a99，其“奥运和”为1000，即S1+S2+…+S99=99×1000=99000．同理根据定义求新数列1，a1，a2，…，a99这100个数“奥运和”．
| S1+S2+…+Sn |
| n |
解答：解：Tn=
对于原数列a1，a2，…，a99
由分析可得：S1+S2+…+S99=99×1000=99000
对于新数列1，a1，a2，…，a99
S1=1
S2=1+a1
S3=1+a1+a2
…
S100=1+a1+a2+…+a99
∴S1+S2+…+S99+S100=1×100+（S1+S2+…+S99）=100+99000=99100
∴T100=
=991
| S1+S2+…+Sn |
| n |
对于原数列a1，a2，…，a99
由分析可得：S1+S2+…+S99=99×1000=99000
对于新数列1，a1，a2，…，a99
S1=1
S2=1+a1
S3=1+a1+a2
…
S100=1+a1+a2+…+a99
∴S1+S2+…+S99+S100=1×100+（S1+S2+…+S99）=100+99000=99100
∴T100=
| S1+S2+…S99+S100 |
| 100 |
点评：本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．关键是找到S1+S2+…+S99+S100=99100．
练习册系列答案
相关题目
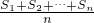为这列数的“奥运和”，现如果有99个数a1+a2+…a99，其“奥运和”为1000，则1，a1，a2，…a99这100个数的“奥运和”为________．
为这列数的“奥运和”，现如果有99个数a1+a2+…a99，其“奥运和”为1000，则1，a1，a2，…a99这100个数的“奥运和”为 ．
为这列数的“奥运和”，现如果有99个数a1+a2+…a99，其“奥运和”为1000，则1，a1，a2，…a99这100个数的“奥运和”为 ．