题目内容
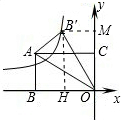
如图，矩形ABOC在坐标系中，A（-3，
），将△ABO沿对角线AO折叠后点B落在B′处，则过点B′的双曲线的解析式为（ ）
| 3 |
A．y=
| B．y=-
| C．y=
| D．y=-
|
过B′点作B′M⊥y轴于M，作B′H⊥x轴于点H，
∵点A（-3，
），
∴OB=3，AB=OC=
，
∴OB′=3．
在Rt△ABO中，tan∠AOB=
=
，
∴∠AOB=30°，
∴∠AOB′=30°，
∴∠B′OM=30°．
在Rt△B′OM中，
∴
=cos30°，
即
=
，
∴OM=
．
∵
=cos60°，
即
=
，
∴OH=
．
∵点B′在第二象限，
∴点B′的坐标为（-
，
），
设过点B′的双曲线的解析式为y=
，
∴k=-
×
=-
．
∴y=y=-
．
故选B．
∵点A（-3，
| 3 |
∴OB=3，AB=OC=
| 3 |
∴OB′=3．
在Rt△ABO中，tan∠AOB=
| AB |
| OB |
| ||
| 3 |
∴∠AOB=30°，
∴∠AOB′=30°，
∴∠B′OM=30°．
在Rt△B′OM中，
∴
| OM |
| 0B′ |
即
| 0M |
| 3 |
| ||
| 2 |
∴OM=
3
| ||
| 2 |
∵
| OH |
| OB′ |
即
| OH |
| 3 |
| 1 |
| 2 |
∴OH=
| 3 |
| 2 |
∵点B′在第二象限，
∴点B′的坐标为（-
| 3 |
| 2 |
3
| ||
| 2 |
设过点B′的双曲线的解析式为y=
| k |
| x |
∴k=-
| 3 |
| 2 |
3
| ||
| 2 |
9
| ||
| 4 |
∴y=y=-
9
| ||
| 4x |
故选B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
