ΧβΡΩΡΎ»ί
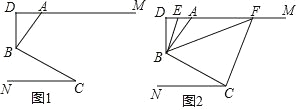
ΓΨΧβΡΩΓΩ“―÷ΣΘΚCD «Ψ≠ΙΐΓœBCAΕΞΒψCΒΡ“ΜΧθ÷±œΏΘ§CAΘΫCB.EΓΔFΖ÷±π «÷±œΏCD…œΝΫΒψΘ§«“ΓœBECΘΫΓœCFAΘΫΓœΠΝ.
(1)»τ÷±œΏCDΨ≠ΙΐΓœBCAΒΡΡΎ≤ΩΘ§«“EΘ§F‘Ύ…δœΏCD…œΘ§»γΆΦ1Θ§»τΓœBCAΘΫ90ΓψΘ§ΓœΠΝΘΫ90ΓψΘ§‘ρBE______CFΘΜ≤ΔΥΒΟςάμ”…Θ°
(2)»γΆΦ2Θ§»τ÷±œΏCDΨ≠ΙΐΓœBCAΒΡΆβ≤ΩΘ§ΓœΠΝΘΫΓœBCAΘ§«κΧα≥ωΙΊ”ΎEFΘ§BEΘ§AF»ΐΧθœΏΕΈ ΐΝΩΙΊœΒΒΡΚœάμ≤¬œκΘΚ__________Θ°≤ΔΥΒΟςάμ”…Θ°
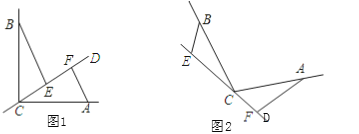
ΓΨ¥πΑΗΓΩΘ®1Θ©=ΘΜΘ®2Θ©EF=BE+AFΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©«σ≥ωΓœBEC=ΓœAFC=90ΓψΘ§ΓœCBE=ΓœACFΘ§ΗυΨίAAS÷ΛΓςBCEΓ’ΓςCAFΘ§ΆΤ≥ωBE=CFΦ¥Ω…ΘΜ
Θ®2Θ©«σ≥ωΓœBEC=ΓœAFCΘ§ΓœCBE=ΓœACFΘ§ΗυΨίAAS÷ΛΓςBCEΓ’ΓςCAFΘ§ΆΤ≥ωBE=CFΘ§CE=AFΦ¥Ω…Θ°
Θ®1Θ©»γΆΦ1÷–Θ§

EΒψ‘ΎFΒψΒΡΉσ≤ύΘ§ΓΏBEΓΆCDΘ§AFΓΆCDΘ§ΓœACB=90ΓψΘ§
ΓύΓœBEC=ΓœAFC=90ΓψΘ§
ΓύΓœBCE+ΓœACF=90ΓψΘ§ΓœCBE+ΓœBCE=90ΓψΘ§
ΓύΓœCBE=ΓœACFΘ§
‘ΎΓςBCEΚΆΓςCAF÷–Θ§
 Θ§
Θ§
ΓύΓςBCEΓ’ΓςCAFΘ®AASΘ©Θ§
ΓύBE=CFΘ§
Θ®2Θ©EF=BE+AFΘ°
άμ”… «ΘΚ»γΆΦ2÷–Θ§

ΓΏΓœBEC=ΓœCFA=ΓœaΘ§Γœa=ΓœBCAΘ§
”÷ΓΏΓœEBC+ΓœBCE+ΓœBEC=180ΓψΘ§ΓœBCE+ΓœACF+ΓœACB=180ΓψΘ§
ΓύΓœEBC+ΓœBCE=ΓœBCE+ΓœACFΘ§
ΓύΓœEBC=ΓœACFΘ§
‘ΎΓςBECΚΆΓςCFA÷–Θ§
 Θ§
Θ§
ΓύΓςBECΓ’ΓςCFAΘ®AASΘ©Θ§
ΓύAF=CEΘ§BE=CFΘ§
ÿEF=CE+CFȧ
ΓύEF=BE+AFΘ°