题目内容
 如图,已知点C为反比例函数
如图,已知点C为反比例函数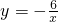 上的一点,连结C0并延长交双曲线的另一个分支于D点,过C点向y轴引垂线,过D点向x轴引垂线,两直线相交于E点,那么△CDE的面积为________.
上的一点,连结C0并延长交双曲线的另一个分支于D点,过C点向y轴引垂线,过D点向x轴引垂线,两直线相交于E点,那么△CDE的面积为________.
12
分析:CE交y轴于M点,DE交x轴于N点,连接OE,根据反比例函数y= (k≠0)中比例系数k的几何意义得到S△OCM=S△ODN=
(k≠0)中比例系数k的几何意义得到S△OCM=S△ODN= |k|=
|k|= ×6=3,根据反比例函数图象的性质得到点C与点D关于原点中心对称,则OM=DN,CM=ON,于是CM=ME,所以S矩形OMEN=2S△OCM=6,然后计算△CDE的面积.
×6=3,根据反比例函数图象的性质得到点C与点D关于原点中心对称,则OM=DN,CM=ON,于是CM=ME,所以S矩形OMEN=2S△OCM=6,然后计算△CDE的面积.
解答:CE交y轴于M点,DE交x轴于N点,连接OE,如图,
则S△OCM=S△ODN= |k|=
|k|= ×6=3,
×6=3,
∵C点与D点是正比例函数与反比例函数的交点,
∴点C与点D关于原点中心对称,
∴OM=DN,CM=ON,
∴CM=ME,
∴S矩形OMEN=2S△OCM=6,
∴S△CDE=3+6+3=12.
故答案为12.
点评:本题考查了反比例函数y= (k≠0)中比例系数k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|.
(k≠0)中比例系数k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|.
分析:CE交y轴于M点,DE交x轴于N点,连接OE,根据反比例函数y=
 (k≠0)中比例系数k的几何意义得到S△OCM=S△ODN=
(k≠0)中比例系数k的几何意义得到S△OCM=S△ODN= |k|=
|k|= ×6=3,根据反比例函数图象的性质得到点C与点D关于原点中心对称,则OM=DN,CM=ON,于是CM=ME,所以S矩形OMEN=2S△OCM=6,然后计算△CDE的面积.
×6=3,根据反比例函数图象的性质得到点C与点D关于原点中心对称,则OM=DN,CM=ON,于是CM=ME,所以S矩形OMEN=2S△OCM=6,然后计算△CDE的面积.解答:CE交y轴于M点,DE交x轴于N点,连接OE,如图,

则S△OCM=S△ODN=
 |k|=
|k|= ×6=3,
×6=3,∵C点与D点是正比例函数与反比例函数的交点,
∴点C与点D关于原点中心对称,
∴OM=DN,CM=ON,
∴CM=ME,
∴S矩形OMEN=2S△OCM=6,
∴S△CDE=3+6+3=12.
故答案为12.
点评:本题考查了反比例函数y=
 (k≠0)中比例系数k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|.
(k≠0)中比例系数k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图,在直角坐标系中,O为坐标原点.已知反比例函数 的图象经过点A(3,m),过点A作
的图象经过点A(3,m),过点A作 轴于点B,
轴于点B, 的面积为
的面积为
【小题1】求k和m的值;
【小题2】点C(x,y)在反比侧函数 的图象上,求当
的图象上,求当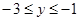 时,对应的x的取值范围;
时,对应的x的取值范围;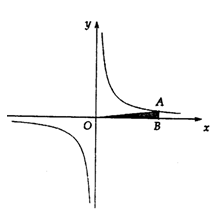
 的图象经过点A(3,m),过点A作
的图象经过点A(3,m),过点A作 轴于点B,
轴于点B, 的面积为
的面积为
【小题1】求k和m的值;
【小题2】点C(x,y)在反比侧函数
 的图象上,求当
的图象上,求当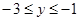 时,对应的x的取值范围;
时,对应的x的取值范围;

 图象上点B处.
图象上点B处. 与x轴、y轴分别交于点E、F,点P为反比例函数在第一象限图象上一动点,PG⊥x轴于G,交线段EF于M,PH⊥y轴于H,交线段EF于N.当点P运动时,∠MON的度数是否改变?如果改变,试说明理由;如果不变,请求其度数.
与x轴、y轴分别交于点E、F,点P为反比例函数在第一象限图象上一动点,PG⊥x轴于G,交线段EF于M,PH⊥y轴于H,交线段EF于N.当点P运动时,∠MON的度数是否改变?如果改变,试说明理由;如果不变,请求其度数.
 的图象经过点A(3,m),过点A作
的图象经过点A(3,m),过点A作 轴于点B,
轴于点B, 的面积为
的面积为
 的图象上,求当
的图象上,求当 时,对应的x的取值范围;
时,对应的x的取值范围;
 的图象经过点A(3,m),过点A作
的图象经过点A(3,m),过点A作 轴于点B,
轴于点B, 的面积为
的面积为
 的图象上,求当
的图象上,求当 时,对应的x的取值范围;
时,对应的x的取值范围;