题目内容
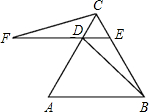 已知△ABC为等边三角形,过AC边上的点D作DE∥AB,交BC与E,在ED的延长线上取点F,使DF=DA,连接FC,BD.
已知△ABC为等边三角形,过AC边上的点D作DE∥AB,交BC与E,在ED的延长线上取点F,使DF=DA,连接FC,BD.
(1)求证:△CEF≌△DCB;
(2)过点F作FG∥DB,交AB于点G,连接CG,请你先补全图形,然后判断△CFG的形状,并证明.
证明:(1)∵EF∥AB,△ABC为等边三角形
∴∠CED=∠CBA=∠ACB=60°,AC=BC
∴△CDE为等边三角形
∴CE=DE=CD
∴AD=BE
又∵FD=AD
∴FD=EB
∴FD+DE=EB+CE
∴EF=BC
又∵∠FEC=∠BCD
∴△CEF≌△DCB(SAS)
(2)
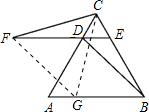
△CFG为等边三角形
证明:∵FG∥DB,FD∥GB
∴四边形FGBD为平行四边形
∴FG=DB,∠DFG=∠DBG
∵△CEF≌△DCB
∴∠EFC=∠CBD,FC=DB
∴∠EFC+∠GFE=∠ABD+∠CBD=∠CBA=60°
FC=FG
∴△CFG为等边三角形.
分析:(1)利用“SAS”全等三角形的判定方法证明;
(2)利用平行四边形的性质:对边相等,对角相等证明.
点评:本题考查了全等三角形的判定、平行线的性质、平行四边形的性质、等边三角形的性质和判定,正确证得△CEF≌△DCB是关键.
∴∠CED=∠CBA=∠ACB=60°,AC=BC
∴△CDE为等边三角形
∴CE=DE=CD
∴AD=BE
又∵FD=AD
∴FD=EB
∴FD+DE=EB+CE
∴EF=BC
又∵∠FEC=∠BCD
∴△CEF≌△DCB(SAS)
(2)

△CFG为等边三角形
证明:∵FG∥DB,FD∥GB
∴四边形FGBD为平行四边形
∴FG=DB,∠DFG=∠DBG
∵△CEF≌△DCB
∴∠EFC=∠CBD,FC=DB
∴∠EFC+∠GFE=∠ABD+∠CBD=∠CBA=60°
FC=FG
∴△CFG为等边三角形.
分析:(1)利用“SAS”全等三角形的判定方法证明;
(2)利用平行四边形的性质:对边相等,对角相等证明.
点评:本题考查了全等三角形的判定、平行线的性质、平行四边形的性质、等边三角形的性质和判定,正确证得△CEF≌△DCB是关键.

练习册系列答案
相关题目
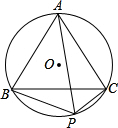 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是

 已知D是等边△ABC外一点,∠BDC=120°,则AD、BD、DC三条线段的数量关系为
已知D是等边△ABC外一点,∠BDC=120°,则AD、BD、DC三条线段的数量关系为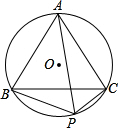 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是 上任一点.
上任一点. 上任一点.
上任一点.