题目内容
解下列方程组或不等式组
(1)
(2)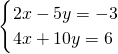
(3)
(4)
解:(1) ,
,
①代入②得,
7x-5(x-3)=9,
解得x=-3,
把x=-3代入①得,
y=-3-3=-6.
于是方程组的解为 .
.
(2)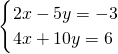 ,
,
①×2+②得,
8x=0,
即x=0,
把x=0代入①得,y= ,
,
于是方程组的解集为: .
.
(3) ,
,
②-①得,3x+3y=3,
即x+y=1③,
③-①得,24x+6y=60,
即4x+y=10④,
④-③得,3x=9,
x=3,
把x=3代入③得,y=-2,
把x=3,y=-2代入①得,
3+2+z=0,
z=-5,
方程组的解为 .
.
分析:(1)先用代入法再用加减消元法求解即可;
(2)先用加减消元法再用代入消元法求解;
(3)先消去z,转化为关于x、y的二元一次方程组解答;
(4)分别求出两个不等式的解集,再求其公共部分即可.
点评:无论解二元一次方程组还是三元一次方程组,其基本思路就是消元,化三元为二元,化二元为一元.
 ,
,①代入②得,
7x-5(x-3)=9,
解得x=-3,
把x=-3代入①得,
y=-3-3=-6.
于是方程组的解为
 .
.(2)
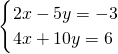 ,
,①×2+②得,
8x=0,
即x=0,
把x=0代入①得,y=
 ,
,于是方程组的解集为:
 .
.(3)
 ,
,②-①得,3x+3y=3,
即x+y=1③,
③-①得,24x+6y=60,
即4x+y=10④,
④-③得,3x=9,
x=3,
把x=3代入③得,y=-2,
把x=3,y=-2代入①得,
3+2+z=0,
z=-5,
方程组的解为
 .
.分析:(1)先用代入法再用加减消元法求解即可;
(2)先用加减消元法再用代入消元法求解;
(3)先消去z,转化为关于x、y的二元一次方程组解答;
(4)分别求出两个不等式的解集,再求其公共部分即可.
点评:无论解二元一次方程组还是三元一次方程组,其基本思路就是消元,化三元为二元,化二元为一元.

练习册系列答案
相关题目
 解下列方程组或不等式组
解下列方程组或不等式组