Question

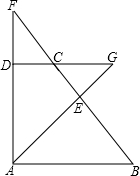如图，在直角梯形ABCD中，AD⊥DC，AB∥DC，AB=BC，AD与BC延长线交于点F，G是DC延长线上一点，AG⊥BC于E．
（1）求证：CF=CG；
（2）连接DE，若

AF

AB

=

3

4

，CD=2，求DE的长．

Answer 1

考点：直角梯形,全等三角形的判定与性质,角平分线的性质,相似三角形的判定与性质

专题：

分析：（1）连接AC，证△ADC≌△AEC，推出DC=CE，再证△FDC≌△GEC即可；
（2）过E作EM⊥AF于M，设AF=3x，AB=BC=4x，在Rt△FAB中，由勾股定理求出BF=5x，求出FC=CG=x，证△FDC∽△FAB，求出x，通过相似求出CE，证
△FCD∽△FEM求出DM，ME，根据勾股定理求出即可．

解答：（1）证明：连接AC，
∵AB=BC，
∴∠BCA=∠CAB，
∵DC∥AB，
∴∠DCA=∠CAB，
∴∠DCA=∠BCA，
∵AD⊥DC，AB∥DC，
∴∠FDC=∠DAB=∠ADC=90°，
∵AG⊥BC，
∴∠CEG=∠CEA=∠ADC=90°，
在△ADC和△AEC中，

∠DCA=∠ECA ∠ADC=∠AEC AC=AC

，
∴△ADC≌△AEC（AAS），
∴CD=CE，
∵∠FDC=∠CEG=90°，
在△FDC和△GEC中，

∠FDC=∠CEG DC=CE ∠FCD=∠GCE

，
∴△FDC≌△GEC（ASA），
∴CF=CG．

（2）解：过E作EM⊥AF于M，
设AF=3x，AB=BC=4x，在Rt△FAB中，由勾股定理得：BF=5x，
则FC=5x-4x=x=CG，
∵DC∥AB，
∴△FDC∽△FAB，
∴

DC

AB

=

FC

FB

，
∴

2

4x

=

x

5x

，
x=2.5，
∴FC=CG=2.5，AB=BC=10，
在Rt△FDC中，DC=2，FC=2.5，由勾股定理得：FD=1.5，
FE=FC+CE=2.5+2，
∵DC∥AB，
∴△FCD∽△FEM，
∴

DC

ME

=

FC

FE

=

FD

FM

∴

2

ME

=

2.5

2+2.5

=

1.5

1.5+DM

∴ME=3.6，DM=1.2，
在Rt△DME中，由勾股定理得：DE=

DM2+ME2

=

1．22+3．62

=

6

5

10

．

点评：本题考查了相似三角形的性质和判定，全等三角形的性质和判定，平行线性质，勾股定理的应用，题目比较好，但是有一点的难度．