题目内容
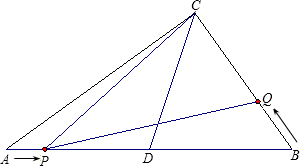
如图,在Rt△ABC中,∠ACB=90°,AC、BC的长为方程x2-14x+a=0的两根,且AC-BC=2,D为AB的中点.
(1)求a的值.
(2)动点P从点A出发,以每秒2个单位的速度,沿A→D→C的路线向点C运动;动点Q从点B出发,以每秒3个单位的速度,沿B→C的路线向点C运动,且点Q每运动1秒,就停止2秒,然后再运动1秒…若点P、Q同时出发,当其中有一点到达终点时整个运动随之结束.设运动时间为t秒.
①在整个运动过程中,设△PCQ的面积为S,试求S与t之间的函数关系式;并指出自变量t的取值范围;
②是否存在这样的t,使得△PCQ为直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
解:(1)∵AC、BC的长为方程x2-14x+a=0的两根,
∴AC+BC=14,
又∵AC-BC=2,
∴AC=8,BC=6,
∴a=8×6=48,
答:a的值是48.
(2)∵∠ACB=90°,
∴AB= =10.
=10.
又∵D为AB的中点,
∴CD= AB=5,
AB=5,
∵sinB= =
= ,
,
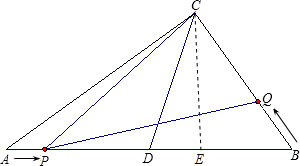
过C作CE⊥AB于E,
根据三角形的面积公式得: AC•BC=
AC•BC= AB•CE,
AB•CE,
6×8=10CE,
解得:CE= ,
,
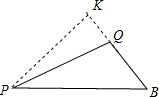
过P作PK⊥BQ于K,
∵sinB= ,
,
∴PK=PB•sinB,
∴S△PBQ= BQ×PK=
BQ×PK= BQ•BPsinB,
BQ•BPsinB,
(I)当0<t≤1时,S=S△ABC-S△ACP-S△PBQ= AC•BC-
AC•BC- AP•CE-
AP•CE- BQ•BPsinB,
BQ•BPsinB,
= ×8×6-
×8×6- ×2t×
×2t× -
- ×3t×(10-2t)×
×3t×(10-2t)× ,
,
= t2-
t2-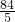 t+24,
t+24,
(II)同理可求:当1<t≤2.5时,S=S△ABC-S△ACP-S△PBQ= AC•BC-
AC•BC- AP•CE-
AP•CE- BQ•BPsinB,
BQ•BPsinB,
= ×8×6-
×8×6- ×2t×
×2t× -
- ×3×(10-2t)×
×3×(10-2t)× ,
,
=- t+12;
t+12;
(III)当2.5<t≤3时,
S= CQ•PCsin∠BCD=
CQ•PCsin∠BCD= ×3×(10-2t)×
×3×(10-2t)× =-
=- t+12;
t+12;
(IIII)当3<t<4时,
∵△PHC∽△BCA,
∴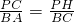 ,
,
∴ =
=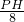 ,
,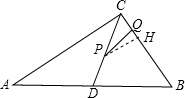
∴PH=8-1.6t,
∴S= CQ•PH=
CQ•PH= CQ•PH=
CQ•PH= ×(6-3t)×(8-1.6t)
×(6-3t)×(8-1.6t)
= t2-
t2-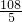 t+48.
t+48.
答:S与t之间的函数关系式是:
S= t2-
t2-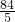 t+24(0<t≤1)
t+24(0<t≤1)
或S=- t+12(1<t≤2.5),
t+12(1<t≤2.5),
或S=- t+12(2.5<t≤3),
t+12(2.5<t≤3),
或S= t2-
t2-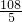 t+48.(3<t<4).
t+48.(3<t<4).
②解:在整个运动过程中,只可能∠PQC=90°,
当P在AD上时,若∠PQC=90°,cosB= =
= ,
,
∴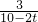 =
= ,
,
∴t=2.5,
当P在DC上时,若∠PQC=90°,
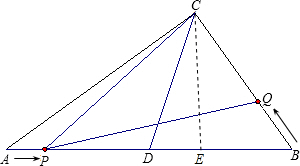 sinA=sin∠CPQ,
sinA=sin∠CPQ,
 =
=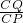 ,
,
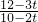 =
= ,或
,或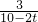 =
= ,
,
t= ,或t=2.5,
,或t=2.5,
∵1<t<4,
∴t= ,t=2.5,符合题意,
,t=2.5,符合题意,
∴当t=2.5秒或 秒时,△PCQ为直角三角形.
秒时,△PCQ为直角三角形.
答:存在这样的t,使得△PCQ为直角三角形,符合条件的t的值是2.5秒, 秒.
秒.
分析:(1)根据根与系数的关系求出AC+BC=14,求出AC和BC,即可求出答案;
(2)根据勾股定理求出AB,sinB,过C作CE⊥AB于E,关键三角形的面积公式求出CE,I当0<t≤1时,S=S△ABC-S△ACP-S△PBQ= AC•BC-
AC•BC- AP•CE-
AP•CE- BQ•BPsinB,求出即可;II同理可求:当1<t≤2.5时,S=S△ABC-S△ACP-S△PBQ=
BQ•BPsinB,求出即可;II同理可求:当1<t≤2.5时,S=S△ABC-S△ACP-S△PBQ= ×8×6-
×8×6- ×2t×
×2t× -
- ×3×(10-2t)×
×3×(10-2t)× =-
=- t+12;III当2.5<t≤3时,S=-
t+12;III当2.5<t≤3时,S=- t+12,IIII当3<t<4时,S=
t+12,IIII当3<t<4时,S= CQ•CPsin∠BCD=
CQ•CPsin∠BCD= CQ•CPsin∠B=
CQ•CPsin∠B= ×(6-3t)×(10-2t)×
×(6-3t)×(10-2t)× =
= t2-
t2-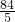 t+24;②在整个运动过程中,只可能∠PQC=90°,当P在AD上时,若∠PQC=90°,cosB=
t+24;②在整个运动过程中,只可能∠PQC=90°,当P在AD上时,若∠PQC=90°,cosB= =
= ,代入即可求出t;当P在DC上时,若∠PQC=90°,sinA=sin∠CPQ,
,代入即可求出t;当P在DC上时,若∠PQC=90°,sinA=sin∠CPQ, =
=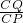 ,得到,
,得到,
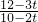 =
= 或
或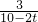 =
= ,求出t,根据t的范围1<t<4,判断即可.
,求出t,根据t的范围1<t<4,判断即可.
点评:本题主要考查对锐角三角函数的定义,根据实际问题列二次函数的解析式,勾股定理,三角形的面积,直角三角形的性质,解一元一次方程,根与系数的关系等知识点的理解和掌握,把实际问题转化成数学问题是解此题的关键,此题是一个拔高的题目,有一定的难度.
∴AC+BC=14,
又∵AC-BC=2,
∴AC=8,BC=6,
∴a=8×6=48,
答:a的值是48.
(2)∵∠ACB=90°,
∴AB=
 =10.
=10.又∵D为AB的中点,
∴CD=
 AB=5,
AB=5,∵sinB=
 =
= ,
,过C作CE⊥AB于E,
根据三角形的面积公式得:
 AC•BC=
AC•BC= AB•CE,
AB•CE,6×8=10CE,
解得:CE=
 ,
,

过P作PK⊥BQ于K,
∵sinB=
 ,
,∴PK=PB•sinB,
∴S△PBQ=
 BQ×PK=
BQ×PK= BQ•BPsinB,
BQ•BPsinB,(I)当0<t≤1时,S=S△ABC-S△ACP-S△PBQ=
 AC•BC-
AC•BC- AP•CE-
AP•CE- BQ•BPsinB,
BQ•BPsinB,=
 ×8×6-
×8×6- ×2t×
×2t× -
- ×3t×(10-2t)×
×3t×(10-2t)× ,
,=
 t2-
t2-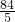 t+24,
t+24,(II)同理可求:当1<t≤2.5时,S=S△ABC-S△ACP-S△PBQ=
 AC•BC-
AC•BC- AP•CE-
AP•CE- BQ•BPsinB,
BQ•BPsinB,=
 ×8×6-
×8×6- ×2t×
×2t× -
- ×3×(10-2t)×
×3×(10-2t)× ,
,=-
 t+12;
t+12;(III)当2.5<t≤3时,
S=
 CQ•PCsin∠BCD=
CQ•PCsin∠BCD= ×3×(10-2t)×
×3×(10-2t)× =-
=- t+12;
t+12;(IIII)当3<t<4时,
∵△PHC∽△BCA,
∴
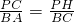 ,
,∴
 =
=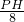 ,
,
∴PH=8-1.6t,
∴S=
 CQ•PH=
CQ•PH= CQ•PH=
CQ•PH= ×(6-3t)×(8-1.6t)
×(6-3t)×(8-1.6t)=
 t2-
t2-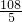 t+48.
t+48.答:S与t之间的函数关系式是:
S=
 t2-
t2-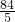 t+24(0<t≤1)
t+24(0<t≤1)或S=-
 t+12(1<t≤2.5),
t+12(1<t≤2.5),或S=-
 t+12(2.5<t≤3),
t+12(2.5<t≤3),或S=
 t2-
t2-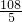 t+48.(3<t<4).
t+48.(3<t<4).②解:在整个运动过程中,只可能∠PQC=90°,
当P在AD上时,若∠PQC=90°,cosB=
 =
= ,
,∴
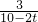 =
= ,
,∴t=2.5,
当P在DC上时,若∠PQC=90°,
 sinA=sin∠CPQ,
sinA=sin∠CPQ, =
=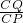 ,
,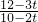 =
= ,或
,或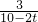 =
= ,
,t=
 ,或t=2.5,
,或t=2.5,∵1<t<4,
∴t=
 ,t=2.5,符合题意,
,t=2.5,符合题意,∴当t=2.5秒或
 秒时,△PCQ为直角三角形.
秒时,△PCQ为直角三角形.答:存在这样的t,使得△PCQ为直角三角形,符合条件的t的值是2.5秒,
 秒.
秒.分析:(1)根据根与系数的关系求出AC+BC=14,求出AC和BC,即可求出答案;
(2)根据勾股定理求出AB,sinB,过C作CE⊥AB于E,关键三角形的面积公式求出CE,I当0<t≤1时,S=S△ABC-S△ACP-S△PBQ=
 AC•BC-
AC•BC- AP•CE-
AP•CE- BQ•BPsinB,求出即可;II同理可求:当1<t≤2.5时,S=S△ABC-S△ACP-S△PBQ=
BQ•BPsinB,求出即可;II同理可求:当1<t≤2.5时,S=S△ABC-S△ACP-S△PBQ= ×8×6-
×8×6- ×2t×
×2t× -
- ×3×(10-2t)×
×3×(10-2t)× =-
=- t+12;III当2.5<t≤3时,S=-
t+12;III当2.5<t≤3时,S=- t+12,IIII当3<t<4时,S=
t+12,IIII当3<t<4时,S= CQ•CPsin∠BCD=
CQ•CPsin∠BCD= CQ•CPsin∠B=
CQ•CPsin∠B= ×(6-3t)×(10-2t)×
×(6-3t)×(10-2t)× =
= t2-
t2-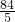 t+24;②在整个运动过程中,只可能∠PQC=90°,当P在AD上时,若∠PQC=90°,cosB=
t+24;②在整个运动过程中,只可能∠PQC=90°,当P在AD上时,若∠PQC=90°,cosB= =
= ,代入即可求出t;当P在DC上时,若∠PQC=90°,sinA=sin∠CPQ,
,代入即可求出t;当P在DC上时,若∠PQC=90°,sinA=sin∠CPQ, =
=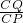 ,得到,
,得到,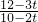 =
= 或
或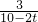 =
= ,求出t,根据t的范围1<t<4,判断即可.
,求出t,根据t的范围1<t<4,判断即可.点评:本题主要考查对锐角三角函数的定义,根据实际问题列二次函数的解析式,勾股定理,三角形的面积,直角三角形的性质,解一元一次方程,根与系数的关系等知识点的理解和掌握,把实际问题转化成数学问题是解此题的关键,此题是一个拔高的题目,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离. 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直. 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA= 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).