题目内容
已知关于x的一元二次方程ax2+bx+1=0(a≠0)有两个相等的实数根,求 的值.
的值.
解:∵ax2+bx+1=0(a≠0)有两个相等的实数根,
∴△=b2-4ac=0,
即b2-4a=0,
b2=4a,
∵ =
= =
= =
=
∵a≠0,
∴ =
= =
=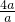 =4.
=4.
分析:由于这个方程有两个相等的实数根,因此△=b2-4a=0,可得出a、b之间的关系,然后将 化简后,用含a的代数式表示b,即可求出这个分式的值.
化简后,用含a的代数式表示b,即可求出这个分式的值.
点评:本题需要综合运用分式和一元二次方程来解决问题,考查学生综合运用多个知识点解决问题的能力,属于中等难度的试题,具有一定的区分度.
∴△=b2-4ac=0,
即b2-4a=0,
b2=4a,
∵
 =
= =
= =
=
∵a≠0,
∴
 =
= =
=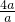 =4.
=4.分析:由于这个方程有两个相等的实数根,因此△=b2-4a=0,可得出a、b之间的关系,然后将
 化简后,用含a的代数式表示b,即可求出这个分式的值.
化简后,用含a的代数式表示b,即可求出这个分式的值.点评:本题需要综合运用分式和一元二次方程来解决问题,考查学生综合运用多个知识点解决问题的能力,属于中等难度的试题,具有一定的区分度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.