Question

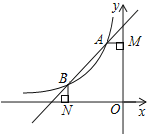
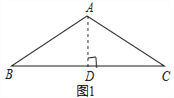
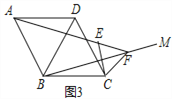
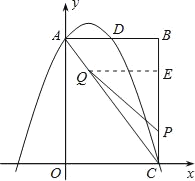
【题目】如图，在矩形OABC中，点O为原点，点A的坐标为(0，8)，点C的坐标为(6，0)．抛物线y＝﹣x2+bx+c经过点A、C，与AB交于点D．

(1)求抛物线的函数解析式；

(2)点P为线段BC上一个动点(不与点C重合)，点Q为线段AC上一个动点，AQ＝CP，连接PQ，设CP＝m，△CPQ的面积为S．

①求S关于m的函数表达式；

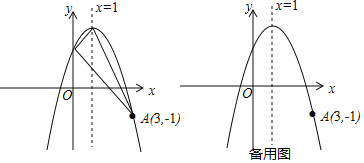
②当S最大时，在抛物线y＝﹣x2+bx+c的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．

Answer 1

【答案】(1)抛物线的解析式为y＝﹣x2+x+8；(2)①S＝﹣m2+3m；②满足条件的点F共有四个，坐标分别为F1(，8)，F2(，4)，F3(，6+)，F4(，6﹣)．

【解析】

（1）运用待定系数法求解；（2）①根据三角函数值性质得；②求函数的最值，根据抛物线性质求出D,Q的坐标，根据直角的位置有3种可能，展开分析，解直角三角形.

(1)将A、C两点坐标代入抛物线，得

，

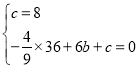解得：，

∴抛物线的解析式为y＝

(2)①∵OA＝8，OC＝6，

∴AC＝

过点Q作QE⊥BC与E点，则sin∠ACB＝

②

∴当m＝5时，S取最大值；

在抛物线对称轴l上存在点F，使△FDQ为直角三角形，

∵抛物线的解析式为y＝的对称轴为x＝，

D的坐标为(3，8)，Q(3，4)，

当∠FDQ＝90°时，F1(，8)，

当∠FQD＝90°时，则F2(，4)，

当∠DFQ＝90°时，设F(，n)，

则FD2+FQ2＝DQ2，

即 +(8﹣n)2+ +(n﹣4)2＝16，

解得：n＝6±，

∴F3(，6+ )，F4(，6﹣)，

满足条件的点F共有四个，坐标分别为

F1(，8)，F2(，4)，F3(，6+ )，F4(，6﹣)．