题目内容
 如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=50°,∠DOE=35°,那么∠BOD是多少度?
(2)如果∠AOE=160°,∠COD=40°,那么∠AOB是多少度?
解:(1)∵OB是∠AOC的平分线,OD是∠COE的平分线
∴∠COD=∠DOE=35°,∠COB=∠BOA=50°
∴∠BOD=∠COD+∠COB=85°;
(2)∵OD是∠COE的平分线,
∴∠COE=2∠COD=2×40°=80°,
∴∠AOC=∠AOE-∠COE=160°-80°=80°,
又∵OB是∠AOC的平分线,
∴∠AOB= .
.
故答案为85°、40°.
分析:(1)可以根据角平分线的定义求得∠COD,∠BOC的度数,即可求∠BOD;
(2)根据角平分线的定义可求∠COE的度数,进而可求∠AOC的度数,再由角平分线即可求解∠AOB.
点评:根据角平分线定义得出所求角与已知角的关系转化求解.
∴∠COD=∠DOE=35°,∠COB=∠BOA=50°
∴∠BOD=∠COD+∠COB=85°;
(2)∵OD是∠COE的平分线,
∴∠COE=2∠COD=2×40°=80°,
∴∠AOC=∠AOE-∠COE=160°-80°=80°,
又∵OB是∠AOC的平分线,
∴∠AOB=
 .
.故答案为85°、40°.
分析:(1)可以根据角平分线的定义求得∠COD,∠BOC的度数,即可求∠BOD;
(2)根据角平分线的定义可求∠COE的度数,进而可求∠AOC的度数,再由角平分线即可求解∠AOB.
点评:根据角平分线定义得出所求角与已知角的关系转化求解.

练习册系列答案
相关题目
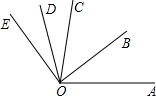 如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
如图所示,OB是∠AOC的平分线,OD是∠COE的平分线. 如图所示,O是△ABC所在平面内一动点,连接OB,OC,并将AB,OB,OC,AC的中点D,E,F,G依次连接,如果DEFG能构成四边形.
如图所示,O是△ABC所在平面内一动点,连接OB,OC,并将AB,OB,OC,AC的中点D,E,F,G依次连接,如果DEFG能构成四边形. 如图所示,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,连接CD交OE于F,则下列结论不能够由上述条件证得的是( )
如图所示,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,连接CD交OE于F,则下列结论不能够由上述条件证得的是( ) 如图所示,OC是∠BOD的平分线,OB是∠AOD的平分线,且∠COD=30°,则∠AOC等于( )
如图所示,OC是∠BOD的平分线,OB是∠AOD的平分线,且∠COD=30°,则∠AOC等于( )