题目内容
一元二次方程（m-1）x2+（m2-4）x+m+5=0的两个实数根互为相反数，则m等于（ ）
| A、-2 | B、±2 | C、-6或1 | D、2 |
分析：设方程的两根是a，b，根据根与系数的关系得到a+b=0，代入求出即可．
解答：解：设方程的两根是a，b，
∵一元二次方程（m-1）x2+（m2-4）x+m+5=0的两个实数根互为相反数，
∴互为相反数的两个数的和为0，
，即由根与系数的关系得：a+b=-
=0，且m-1≠0，
∴m=±2．
故选B．
∵一元二次方程（m-1）x2+（m2-4）x+m+5=0的两个实数根互为相反数，
∴互为相反数的两个数的和为0，
，即由根与系数的关系得：a+b=-
| m2-4 |
| m-1 |
∴m=±2．
故选B．
点评：本题主要考查对一元二次方程的定义，根与系数的关系等知识点的理解和掌握，能得出-
=0和m-1≠0是解此题的关键．
| m2-4 |
| m-1 |
练习册系列答案
名校课堂系列答案
相关题目
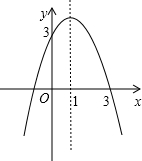已知二次函数y=-x2+bx+c的图象如图所示，解决下列问题：
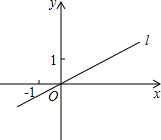如图，在平面直角坐标系中，直线l的解析式为y=