题目内容
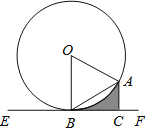
【题目】如图，
的半径
，AB是弦，直线EF经过点B，
于点C，
．
求证：EF是的切线；
若
，求AB的长；
在的条件下，求图中阴影部分的面积．
【答案】（1）证明见解析（2）2（3）
【解析】分析：1）由OA=OB得到∠OAB=∠OBA，加上∠BAC=∠OAB，则∠BAC=∠OBA，于是可判断OB∥AC，由于AC⊥EF，所以OB⊥EF，则可根据切线的判定定理得到EF是⊙O的切线；
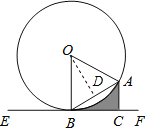
（2）过点O作OD⊥AB于点D，根据垂径定理得AD=
AB，再证明Rt△AOD∽Rt△ABC，利用相似比可计算出AB=2；
（3）由AB=OB=OC=2可判断△OAB为等边三角形，则∠AOB=60°，则∠ABC=30°，则可计算出BC=
AC=，然后根据三角形面积公式和扇形面积公式，利用S阴影部分=S四边形AOBC-S扇形OAB=S△AOB+S△ABC-S扇形OAB进行计算即可．
详解：
证明：
，
，
，
，
，
，
，
是
的切线；
过点O作
于点D，则
，
，
∽
，
，即
，
；
，
为等边三角形，
，
，
，
，
∴
=
=
练习册系列答案
走进文言文系列答案
相关题目
