题目内容
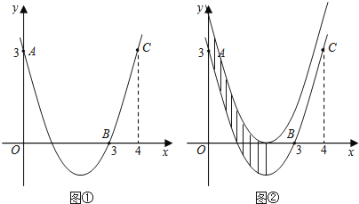
【题目】一次函数![]() 的图象经过第一、二、三象限,且与反比例函数图象相交于
的图象经过第一、二、三象限,且与反比例函数图象相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
, ![]() .且点
.且点![]() 横坐标是点
横坐标是点![]() 纵坐标的2倍.
纵坐标的2倍.
(1)求反比例函数的解析式;
(2)设点![]() 横坐标为
横坐标为![]() ,
, ![]() 面积为
面积为![]() ,
,
求![]() 与
与![]() 的函数关系式,并求出自变量的取值范围.
的函数关系式,并求出自变量的取值范围.

【答案】(1) ![]() ; (2)当m<-2或0<m<2时,s=
; (2)当m<-2或0<m<2时,s=![]() –
–![]()
【解析】试题分析:由题意仅能确定点B位于第一象限或第三象限,所以求解的时候需要对点B位于哪一象限进行分类讨论,①(1)当点B位于第一象限,作BD⊥x轴交x轴于点D,设B(2a,a),a>0,由OB=![]() 结合勾股定理可以求出a的值,从而求出点B的坐标,即可求出反比例函数解析式;(2)先求出直线AB的解析式,进而求出点C的坐标,同时确定m的范围,由S△AOB=S△AOC+S△BOC得出S关于m的函数关系式;②当点B位于第三象限,同上进行求解即可.
结合勾股定理可以求出a的值,从而求出点B的坐标,即可求出反比例函数解析式;(2)先求出直线AB的解析式,进而求出点C的坐标,同时确定m的范围,由S△AOB=S△AOC+S△BOC得出S关于m的函数关系式;②当点B位于第三象限,同上进行求解即可.
试题解析:
由于点B的横坐标是纵坐标的2倍,所以反比例函数只能位于一、三象限.
①点B位于第一象限,作BD⊥x轴交x轴于点D,

(1)设B(2a,a),a>0,
∵OB=![]() ,∴OB2=a2+(2a)2=5,解得a=1,
,∴OB2=a2+(2a)2=5,解得a=1,
∴B(2,1),
∴反比例函数解析式为:y=![]() ;
;
(2)A(m, ![]() ),m<0,
),m<0,
设直线AB解析式为:y1=k1x+b1,
 ,
,
解得 ,
,
∴y1=-![]() x+1+
x+1+![]() ,
,
令x=0,y=1+![]() >0 ,
>0 ,
∴![]() >-1,∴m<-2,
>-1,∴m<-2,
∴OC=1+![]() ,
,
∴S△AOB=S△AOC+S△BOC=![]() (1+
(1+![]() )×2+
)×2+![]() (1+
(1+![]() )×(-m)=
)×(-m)=![]() -
-![]() ,
,
即当m<-2时,S=![]() -
-![]() ;
;
②点B位于第三象限时,同上可求出点B(-2,-1) ,

(1)反比例函数解析式为:y=![]() ;
;
(2)A(m, ![]() ),m>0,
),m>0,
设直线AB解析式为:y2=k2x+b2,
 ,
,
解得 ,
,
∴y2=![]() x+
x+![]() -1,
-1,
令x=0,y=![]() -1>0 ,
-1>0 ,
∴![]() >1,∴0<m<2,
>1,∴0<m<2,
∴OC=![]() -1,
-1,
∴S△AOB=S△AOC+S△BOC=![]() (
(![]() -1)×m+
-1)×m+![]() (
(![]() -1)×2=
-1)×2=![]() -
-![]() ,
,
即当0<m<2时,S=![]() -
-![]() ;
;
综上所述:(1)y=![]() ;(2)m<-2或0<m<2时,S=
;(2)m<-2或0<m<2时,S=![]() -
-![]() .
.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案