题目内容
如图,抛物线 交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.
交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.
(1)请直接写出抛物线y2的解析式;
(2)若点P是x轴上一动点,且满足∠CPA=∠OBA,求出所有满足条件的P点坐标;
(3)在第四象限内抛物线y2上,是否存在点Q,使得△QOC中OC边上的高h有最大值?若存在,请求出点Q的坐标及h的最大值;若不存在,请说明理由.
解:(1)抛物线 向右平移4个单位的顶点坐标为(4,-1),
向右平移4个单位的顶点坐标为(4,-1),
∴抛物线y2的解析式为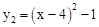 。
。
(2)当x=0时,y1=﹣1,y1=0时,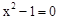 =0,解得x=1或x=-1,
=0,解得x=1或x=-1,
∴点A(1,0),B(0,-1)。∴∠OBA=450。
联立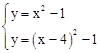 ,解得
,解得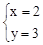 。
。
∴点C的坐标为(2,3)。
∵∠CPA=∠OBA,
∴点P在点A的左边时,坐标为(-1,0);在点A的右边时,坐标为(5,0)。
∴点P的坐标为(-1,0)或(5,0)。
(3)存在。
∵点C(2,3),∴直线OC的解析式为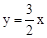 ,
,
设与OC平行的直线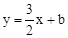 ,
,
联立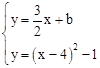 ,消掉y得,
,消掉y得,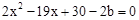 ,
,
当△=0,方程有两个相等的实数根时,△QOC中OC边上的高h有最大值,
此时,由一元二次方程根与系数的关系,得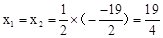 ,
,
∴此时,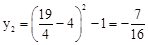 。
。
∴存在第四象限的点Q(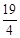 ,
,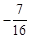 ),使得△QOC中OC边上的高h有最大值,
),使得△QOC中OC边上的高h有最大值,
此时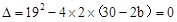 ,解得
,解得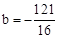 。
。
∴过点Q与OC平行的直线解析式为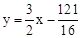 。
。
令y=0,则 ,解得
,解得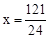 。
。
设直线与x轴的交点为E,则E(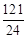 ,0)。
,0)。
过点C作CD⊥x轴于D,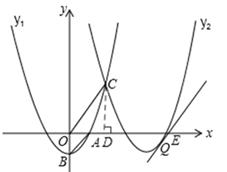
根据勾股定理,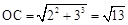 ,
,
则由面积公式,得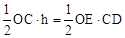 ,即
,即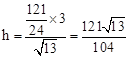 。
。
∴存在第四象限的点Q(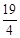 ,
,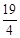 ),使得△QOC中OC边上的高h有最大值,最大值为
),使得△QOC中OC边上的高h有最大值,最大值为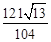 。
。
解析

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
| 销售单价(元) | x |
| 销售量y(件) | |
| 销售玩具获得利润w(元) | |
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
 是函数
是函数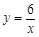 在第一象限内的图象,抛物线是函数
在第一象限内的图象,抛物线是函数 的图象.点
的图象.点 (
( )在曲线
)在曲线 都是整数.
都是整数.
 ;
; 中任取两点作直线,求所有不同直线的条数;
中任取两点作直线,求所有不同直线的条数; 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经 ),点M是抛物线C2:
),点M是抛物线C2: (
( <0)的顶点.
<0)的顶点.

 (a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.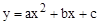 经过A,B,C三点,顶点为F.
经过A,B,C三点,顶点为F.

 )为圆心,以2为半径的圆与x轴交于A,B两点.
)为圆心,以2为半径的圆与x轴交于A,B两点.