Question

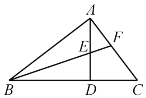
【题目】（1）如图，在中，已知，，与的平分线交于点，求证：是等腰三角形．

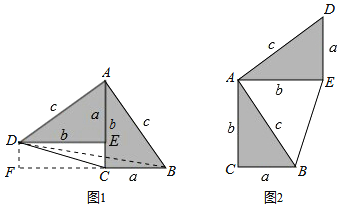
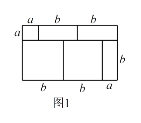
（2）.阅读下列文字：我们知道，对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式．例如由图1可以得到 ．请解答下列问题：

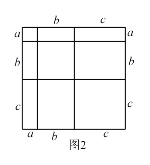
①.写出图2中所表示的数学等式；

②.利用（1）中所得到的结论，解决下面的问题：已知，，求的值；

Answer 1

【答案】（1）见解析；（2）①；②60.

【解析】

（1）根据“，”得出∠AFB=∠BED，又∠BED=∠AEF，即可得出答案；

（2）①直接求得正方形的面积，然后再根据正方形的面积=各矩形的面积之和求解即可得出答案；②将，代入①中得到的关系式，然后进行计算即可得出答案.

（1）证明：∵

∴∠ABF+∠AFB=90°

又∵

∴∠EBD+∠BED=90°

又与的平分线交于点

∴∠ABF=∠EBD

∴∠AFB=∠BED

又∠BED=∠AEF

∴∠AFB=∠AEF

∴△AEF为等腰三角形.

（2）①正方形的面积=

各矩形的面积之和=

∵正方形的面积=各矩形的面积之和

∴

②∵，

由①可知：