题目内容
(14分)如图,在□ABCD中,![]() ,
,![]() .点
.点![]() 由
由![]() 出发沿
出发沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,线段
;同时,线段![]() 由
由![]() 出发沿
出发沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() 、
、![]() .若设运动时间为
.若设运动时间为![]() (s)(
(s)(![]() ).解答下列问题:
).解答下列问题:
(1)当![]() 为何值时,
为何值时,![]() ∥
∥![]() ?并求出此时
?并求出此时![]() 的长;
的长;
(2)试判断△![]() 的形状,并请说明理由.
的形状,并请说明理由.
(3)当![]() 时,
时,
(ⅰ)在上述运动过程中,五边形![]() 的面积 ▲ (填序号)
的面积 ▲ (填序号)
①变大 ②变小 ③先变大,后变小 ④不变
(ⅱ)设![]() 的面积为
的面积为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式及
之间的函数关系式及![]() 的取值范围.
的取值范围.
解:(1)由题意知![]() ,
,![]() ,
,
在□![]() 中,
中,![]() ,
,![]() ,
,
当![]() ∥
∥![]() 时,
时,![]() ∽
∽![]() ,∴
,∴![]() ,∴
,∴![]() …………………3分
…………………3分
(或当![]() ∥
∥![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() )
)
此时,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,
∴![]() ……………………………………4分
……………………………………4分
(2)△![]() 是等腰三角形 ………………………………………………………5分
是等腰三角形 ………………………………………………………5分
证明:在□![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ∥
∥![]() ,∴
,∴![]()
∴![]() ∴
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ∥
∥![]() ,∴
,∴![]() ,
,
∴![]() ≌
≌![]() ,∴
,∴![]() ……8分
……8分
(3) (ⅰ)在上述运动过程中,五边形![]() 的面积 ④ (填序号)…………10分
的面积 ④ (填序号)…………10分
(ⅱ) ∵△![]() ∽△
∽△![]() ,∴
,∴![]() ,∴
,∴![]() …………11分
…………11分
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
∴△![]() ∽△
∽△![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() ……………13分
……………13分
∴当![]() 时,
时,![]()
![]() ,
,
∴![]() ……………………………………14分
……………………………………14分
(其它解法,正确合理可参照给分。)
解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=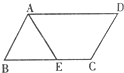 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.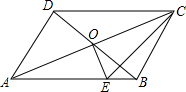 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是