题目内容
 已知:△ABC中,AC⊥BC,CE⊥AB于E,AF平分∠CAB交CE于F,过F作FD∥BC交AB于D.
已知:△ABC中,AC⊥BC,CE⊥AB于E,AF平分∠CAB交CE于F,过F作FD∥BC交AB于D.
求证:AC=AD.
证明:∵CE⊥AB,∠ACB=90°,
∴∠CEB=90°,
∴∠ACE+∠BCE=90°,∠B+∠BCE=90°,
∴∠B=∠ACE,
∵FD∥BC,
∴∠B=∠ADF=∠ACE,
∵AF平分∠CAB,
∴∠CAF=∠DAF,
在△ACF和△ADF中
 ,
,
∴△ACF≌△ADF,
∴AC=AD.
分析:求出∠ACE=∠B,根据平行线性质求出∠B=∠ADF=∠ACE,根据ASA证△ACF≌△ADF即可.
点评:本题考查了平行线性质,三角形的内角和定理,全等三角形的性质和判定的应用,关键是证出△ACF≌△ADF,主要培养了学生的推理能力.
∴∠CEB=90°,
∴∠ACE+∠BCE=90°,∠B+∠BCE=90°,
∴∠B=∠ACE,
∵FD∥BC,
∴∠B=∠ADF=∠ACE,
∵AF平分∠CAB,
∴∠CAF=∠DAF,
在△ACF和△ADF中
 ,
,∴△ACF≌△ADF,
∴AC=AD.
分析:求出∠ACE=∠B,根据平行线性质求出∠B=∠ADF=∠ACE,根据ASA证△ACF≌△ADF即可.
点评:本题考查了平行线性质,三角形的内角和定理,全等三角形的性质和判定的应用,关键是证出△ACF≌△ADF,主要培养了学生的推理能力.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
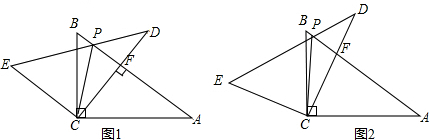
 如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示)
如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示) 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.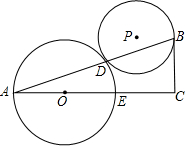 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,