题目内容
一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
| x | 3O00 | 3200 | 3500 | 4000 |
| y | 100 | 96 | 90 | 80 |
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
| 租出的车辆数 | ______ | 未租出的车辆数 | ______ |
| 租出每辆车的月收益 | ______ | 所有未租出的车辆每月的维护费 | ______ |
解:(1)由表格数据可知y与x是一次函数关系,
设其解析式为y=kx+b.
由题:
解之得:
∴y与x间的函数关系是 .
.
(2)如下表:
(3)设租赁公司获得的月收益为W元,依题意可得:
W=(- +160)(x-150)-(x-3000)
+160)(x-150)-(x-3000)
=(-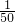 x2+163x-24000)-(x-3000)
x2+163x-24000)-(x-3000)
=-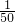 x2+162x-21000
x2+162x-21000
=-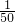 (x-4050)2+307050
(x-4050)2+307050
当x=4050时,Wmax=307050,
即:当每辆车的月租金为4050元时,公司获得最大月收益307050元.
故答案为: ,
, .
.
分析:(1)判断出y与x的函数关系为一次函数关系,再根据待定系数法求出函数解析式;
(2)根据题意可用代数式求出出租车的辆数和未出租车的辆数即可.
(3)租出的车的利润减去未租出车的维护费,即为公司最大月收益.
点评:本题考查了二次函数应用和一次函数应用,表示出(2)中的表达式是解题的关键.
设其解析式为y=kx+b.
由题:

解之得:

∴y与x间的函数关系是
 .
.(2)如下表:
| 租出的车辆数 |  | 未租出的车辆数 |  |
| 租出的车每辆的月收益 | x-150 | 所有未租出的车辆每月的维护费 | x-3000 |
W=(-
 +160)(x-150)-(x-3000)
+160)(x-150)-(x-3000)=(-
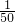 x2+163x-24000)-(x-3000)
x2+163x-24000)-(x-3000)=-
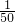 x2+162x-21000
x2+162x-21000=-
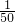 (x-4050)2+307050
(x-4050)2+307050当x=4050时,Wmax=307050,
即:当每辆车的月租金为4050元时,公司获得最大月收益307050元.
故答案为:
 ,
, .
.分析:(1)判断出y与x的函数关系为一次函数关系,再根据待定系数法求出函数解析式;
(2)根据题意可用代数式求出出租车的辆数和未出租车的辆数即可.
(3)租出的车的利润减去未租出车的维护费,即为公司最大月收益.
点评:本题考查了二次函数应用和一次函数应用,表示出(2)中的表达式是解题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目