��Ŀ����
�磨ͼ1������ƽ��ֱ������ϵ�У���֪�� ����
���� ��x�������ϣ���
��x�������ϣ��� ������
������ ���߶�
���߶� �ϴ�
�ϴ� ����B����ÿ��
����B����ÿ�� ����λ���ٶ��˶�����M��N��x�ᣨM�ڵ�N����ࣩ����P��M��NΪ������������ǵȱ������Σ����˶�ʱ��Ϊ�룮
����λ���ٶ��˶�����M��N��x�ᣨM�ڵ�N����ࣩ����P��M��NΪ������������ǵȱ������Σ����˶�ʱ��Ϊ�룮
��1�� ��ֱ�� �Ľ���ʽ��
�Ľ���ʽ��
��2����ȱ� �ı߳�����
�ı߳����� �Ĵ���ʽ��ʾ������������ȱ�
�Ĵ���ʽ��ʾ������������ȱ� �Ķ���
�Ķ��� �˶�����ԭ��
�˶�����ԭ�� �غ�ʱ
�غ�ʱ ��ֵ��
��ֵ��
��3�����ȡ ���е�
���е� ����
���� ����
Ϊ���� �ڲ�����ͼ2��ʾ�ľ���
�ڲ�����ͼ2��ʾ�ľ���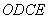 ����
���� ���߶�
���߶� �ϣ���ȱ�
�ϣ���ȱ� �;���
�;��� �ص����ֵ����Ϊ
�ص����ֵ����Ϊ ���������
��������� ��ʱ
��ʱ ��
�� �ĺ�����ϵʽ�������
�ĺ�����ϵʽ������� �����ֵ��
�����ֵ��
 ����
���� ��x�������ϣ���
��x�������ϣ��� ������
������ ���߶�
���߶� �ϴ�
�ϴ� ����B����ÿ��
����B����ÿ�� ����λ���ٶ��˶�����M��N��x�ᣨM�ڵ�N����ࣩ����P��M��NΪ������������ǵȱ������Σ����˶�ʱ��Ϊ�룮
����λ���ٶ��˶�����M��N��x�ᣨM�ڵ�N����ࣩ����P��M��NΪ������������ǵȱ������Σ����˶�ʱ��Ϊ�룮 ��1�� ��ֱ��
 �Ľ���ʽ��
�Ľ���ʽ�� ��2����ȱ�
 �ı߳�����
�ı߳����� �Ĵ���ʽ��ʾ������������ȱ�
�Ĵ���ʽ��ʾ������������ȱ� �Ķ���
�Ķ��� �˶�����ԭ��
�˶�����ԭ�� �غ�ʱ
�غ�ʱ ��ֵ��
��ֵ�� ��3�����ȡ
 ���е�
���е� ����
���� ����
Ϊ���� �ڲ�����ͼ2��ʾ�ľ���
�ڲ�����ͼ2��ʾ�ľ��� ����
���� ���߶�
���߶� �ϣ���ȱ�
�ϣ���ȱ�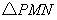 �;���
�;��� �ص����ֵ����Ϊ
�ص����ֵ����Ϊ ���������
��������� ��ʱ
��ʱ ��
�� �ĺ�����ϵʽ�������
�ĺ�����ϵʽ������� �����ֵ��
�����ֵ��
�⣺��1��ֱ�ߵĽ���ʽΪ�� �� ����2��  �� �� �� �� �� �� �� �� �� �� �ǵȱ������Σ� �ǵȱ������Σ� �� �� �� �� �� ������  ���N�غ�ʱ�� ���N�غ�ʱ�� �� �� �� �� �� �� �� ����3���ٵ�  ʱ����ͼ2�� ʱ����ͼ2����  �� �� �ڵ�H���ص�����Ϊֱ������ �ڵ�H���ص�����Ϊֱ������ �� ����  �� �� �� �� �� �� �� �� �� �� �� �� �� �� �� �� �� ��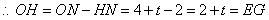 �� �� �� �� �� �� ����������� �������������  ʱ�� ʱ�� �� �� �ڵ�  ʱ����ͼ3�� ʱ����ͼ3����  �� �� �ڵ� �ڵ� ���� ���� �ڵ� �ڵ� �� �� �� �� �ڵ�G���ص�����Ϊ����� �ڵ�G���ص�����Ϊ����� ���� ���� �� �� �� �� �� �� �� �� �� �� �� �� ���൱ ���൱ ʱ�� ʱ�� �����ֵ�� �����ֵ�� �� �� �۵�  ʱ�� ʱ�� ���� ���� ��D�غϣ��� ��D�غϣ��� �� �� �ڵ� �ڵ� �� �� �� �� �ڵ�G���ص�����Ϊ�������� �ڵ�G���ص�����Ϊ�������� ����ͼ4�� ����ͼ4�� �� ��������������  ʱ�� ʱ�� ���� ���� ʱ�� ʱ�� ���� ���� ʱ�� ʱ�� �� �� ����S�����ֵ�� ����S�����ֵ�� �� �� |
|

��ϰ��ϵ�д�
 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�
�����Ŀ



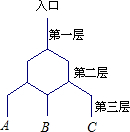 ��ͼ��ʾ������ֱƽ���ڵ�һ����ͨ����Ϸ����ͼ����ֱ�߶κ�б�߶ζ���ʾͨ���������ڽ��㴦����������ֱ�߶���һ����Ϊ��һ�㣬�ж�����Ϊ�ڶ��㣬�������ƣ�����һ��С���Ӵӵ�һ���ͨ���������˶�������С��������ÿһ��ͨ���Ŀ�������ͬ�����С���Ӵӵ�����ͨ���ij���B�ѳ��ĸ���Ϊ
��ͼ��ʾ������ֱƽ���ڵ�һ����ͨ����Ϸ����ͼ����ֱ�߶κ�б�߶ζ���ʾͨ���������ڽ��㴦����������ֱ�߶���һ����Ϊ��һ�㣬�ж�����Ϊ�ڶ��㣬�������ƣ�����һ��С���Ӵӵ�һ���ͨ���������˶�������С��������ÿһ��ͨ���Ŀ�������ͬ�����С���Ӵӵ�����ͨ���ij���B�ѳ��ĸ���Ϊ