题目内容
 如图,点A、B在⊙O上,且AB=BO.∠ABO的平分线与AO相交于点C,若AC=3,则⊙O的周长为________.(结果保留π)
如图,点A、B在⊙O上,且AB=BO.∠ABO的平分线与AO相交于点C,若AC=3,则⊙O的周长为________.(结果保留π)
12π
分析:先由三边相等的三角形是等边三角形得出△OAB是等边三角形,再根据等腰三角形三线合一的性质得出OA=2AC=6,然后根据圆的周长公式计算即可.
解答:∵OA=OB,AB=BO,
∴OA=OB=AB,即△OAB是等边三角形,
∵BC平分∠ABO,
∴OA=2AC=6,
∴⊙O的周长为2π•OA=2π×6=12π.
故答案为12π.
点评:本题主要考查了等边三角形的判定与性质,圆的基本性质及周长,难度适中.
分析:先由三边相等的三角形是等边三角形得出△OAB是等边三角形,再根据等腰三角形三线合一的性质得出OA=2AC=6,然后根据圆的周长公式计算即可.
解答:∵OA=OB,AB=BO,
∴OA=OB=AB,即△OAB是等边三角形,
∵BC平分∠ABO,
∴OA=2AC=6,
∴⊙O的周长为2π•OA=2π×6=12π.
故答案为12π.
点评:本题主要考查了等边三角形的判定与性质,圆的基本性质及周长,难度适中.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目


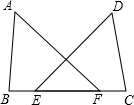 如图,点E、F在BC上,AB=DC,∠B=∠C,∠A=∠D,
如图,点E、F在BC上,AB=DC,∠B=∠C,∠A=∠D,
 如图,点C、D在线段AB上,且C为AB的一个四等分点,D为AC中点,若BC=2,则BD的长为
如图,点C、D在线段AB上,且C为AB的一个四等分点,D为AC中点,若BC=2,则BD的长为