题目内容
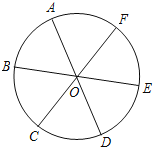
【题目】如图所示，∠B=∠OAF=90°，BO=3cm，AB=4cm，AF=12cm，求图中半圆的面积．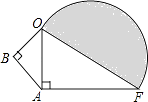
【答案】解：如图，∵在直角△ABO中，∠B=90°，BO=3cm，AB=4cm，
∴AO= 
=5cm．
则在直角△AFO中，由勾股定理得到：FO= 
=13cm，
∴图中半圆的面积= 
π×（ 
）2= π× 
= 
（cm2）．
答：图中半圆的面积是 cm2 ．
【解析】首先，在直角△ABO中，利用勾股定理求得AO=5cm；然后在直角△AFO中，由勾股定理求得斜边FO的长度；最后根据圆形的面积公式进行解答．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
练习册系列答案
相关题目
