题目内容
 如图
如图
(1)求反比例函数和一次函数解析式;
(2)根据图象写出反比例函数值大于一次函数值x的取值范围.
解:(1)将N(-1,-4)代入反比例函数y= 中得:-4=
中得:-4= ,
,
解得:k=4,
故反比例函数解析式为y= ,
,
将M的坐标(2,m)代入反比例解析式得:m= =2,
=2,
则M(2,2),
将M(2,2)和N(-1,-4)代入一次函数解析式y=ax+b得: ,
,
解得: ,
,
故一次函数解析式为y=y=2x-2;
(2)由图形可得:当x<-1或0<x<2时,反比例函数值大于一次函数值.
分析:(1)将N的坐标代入反比例解析式中,求出k的值,确定出反比例函数解析式,将M的坐标代入确定出的反比例解析式中求出m的值,确定出M的坐标,将M和N的坐标代入一次函数y=ax+b中,求出a与b的值,即可确定出一次函数解析式;
(2)由M和N的横坐标为-1和2,以及0,将x轴分为四个范围,找出反比例函数图象在一次函数图象上方时x的范围即可.
点评:此题考查了反比例函数与一次函数的交点问题,利用了待定系数法及数形结合的思想,待定系数法是数学中重要的思想方法,学生做题时注意灵活运用.
 中得:-4=
中得:-4= ,
,解得:k=4,
故反比例函数解析式为y=
 ,
,将M的坐标(2,m)代入反比例解析式得:m=
 =2,
=2,则M(2,2),
将M(2,2)和N(-1,-4)代入一次函数解析式y=ax+b得:
 ,
,解得:
 ,
,故一次函数解析式为y=y=2x-2;
(2)由图形可得:当x<-1或0<x<2时,反比例函数值大于一次函数值.
分析:(1)将N的坐标代入反比例解析式中,求出k的值,确定出反比例函数解析式,将M的坐标代入确定出的反比例解析式中求出m的值,确定出M的坐标,将M和N的坐标代入一次函数y=ax+b中,求出a与b的值,即可确定出一次函数解析式;
(2)由M和N的横坐标为-1和2,以及0,将x轴分为四个范围,找出反比例函数图象在一次函数图象上方时x的范围即可.
点评:此题考查了反比例函数与一次函数的交点问题,利用了待定系数法及数形结合的思想,待定系数法是数学中重要的思想方法,学生做题时注意灵活运用.

练习册系列答案
相关题目
 B(3,m)两点.
B(3,m)两点.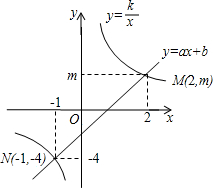 (2008•淮北模拟)如图
(2008•淮北模拟)如图 如图,一次函数y=ax+b与反比例函数y=
如图,一次函数y=ax+b与反比例函数y=