题目内容
 如图,AB为⊙O的弦,∠AOB=100°,点C在⊙O上,且
如图,AB为⊙O的弦,∠AOB=100°,点C在⊙O上,且 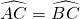 ,则∠CAB的度数为________.
,则∠CAB的度数为________.
65°
分析:作辅助线BC构建等腰三角形ABC、圆周角∠ACB;由同弧所对的圆周角等于所对的圆心角的一半,知∠ACB=50°,然后在等腰三角形ACB中根据三角形的内角和定理求得∠CAB的度数.
解答: 解:连接BC.
解:连接BC.
∵∠AOB=100°,
∴∠ACB= ∠AOB=50°(同弧所对的圆周角等于所对的圆心角的一半);
∠AOB=50°(同弧所对的圆周角等于所对的圆心角的一半);
又∵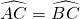 ,
,
∴AC=BC,
∴∠CAB=∠CBA(等边对等角),
∴∠CAB= (180°-∠ACB)=65°(三角形内角和定理).
(180°-∠ACB)=65°(三角形内角和定理).
故答案是:65°.
点评:本题考查了圆周角定理,圆心角、弧、弦的关系.在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
分析:作辅助线BC构建等腰三角形ABC、圆周角∠ACB;由同弧所对的圆周角等于所对的圆心角的一半,知∠ACB=50°,然后在等腰三角形ACB中根据三角形的内角和定理求得∠CAB的度数.
解答:
 解:连接BC.
解:连接BC.∵∠AOB=100°,
∴∠ACB=
 ∠AOB=50°(同弧所对的圆周角等于所对的圆心角的一半);
∠AOB=50°(同弧所对的圆周角等于所对的圆心角的一半);又∵
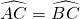 ,
,∴AC=BC,
∴∠CAB=∠CBA(等边对等角),
∴∠CAB=
 (180°-∠ACB)=65°(三角形内角和定理).
(180°-∠ACB)=65°(三角形内角和定理).故答案是:65°.
点评:本题考查了圆周角定理,圆心角、弧、弦的关系.在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
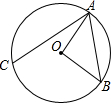 如图,AB为⊙O的弦,∠AOB=100°,点C在⊙O上,且
如图,AB为⊙O的弦,∠AOB=100°,点C在⊙O上,且 
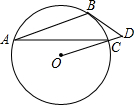 已知:如图,AB为⊙O的弦,过点O作AB的平行线,交⊙O于点C,直线OC上一点D满足∠D=∠ACB.
已知:如图,AB为⊙O的弦,过点O作AB的平行线,交⊙O于点C,直线OC上一点D满足∠D=∠ACB. 54、如图,AB为⊙O的弦,C、D为直线AB上两点,要使OC=OD,则图中的线段必满足的条件是
54、如图,AB为⊙O的弦,C、D为直线AB上两点,要使OC=OD,则图中的线段必满足的条件是 (2012•闵行区三模)已知:如图,AB为⊙O的弦,OD⊥AB,垂足为点D,DO的延长线交⊙O于点C.过点C作CE⊥AO,分别与AB、AO的延长线相交于E、F两点.CD=8,sin∠A=
(2012•闵行区三模)已知:如图,AB为⊙O的弦,OD⊥AB,垂足为点D,DO的延长线交⊙O于点C.过点C作CE⊥AO,分别与AB、AO的延长线相交于E、F两点.CD=8,sin∠A= 如图,AB为⊙0的弦,⊙0的半径为10,0C⊥AB于点D,交⊙0于点C,且CD=2,则弦AB的长是
如图,AB为⊙0的弦,⊙0的半径为10,0C⊥AB于点D,交⊙0于点C,且CD=2,则弦AB的长是