题目内容
已知在△ABC中,AC=3,BC=4,∠C=90°,建立以点A为坐标原点,使AB落在x轴的负半轴上的平面直角坐标系,则点C的坐标为
- A.
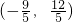
- B.
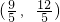 或
或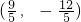
- C.
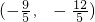
- D.
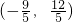 或
或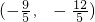
D
分析:利用勾股定理列式求出AB的长,再过点C作CD⊥AB于D,利用△ACD和△ABC相似,利用相似三角形对应边成比例列式求出AD、CD的长,再分点C在第二象限和第三象限两种情况讨论求解即可.
解答: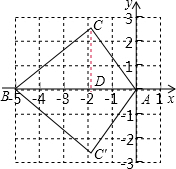 解:如图,∵AC=3,BC=4,∠C=90°,
解:如图,∵AC=3,BC=4,∠C=90°,
∴AB= =
= =5,
=5,
过点C作CD⊥AB于D,
则△ACD∽△ABC,
∴ =
= =
= ,
,
即 =
=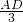 =
= ,
,
解得CD= ,AD=
,AD= ,
,
当点C在第二象限时,点C的坐标为(- ,
, ),
),
当点C在第三象限时,点C的坐标为(- ,-
,- ),
),
综上所述,点C的坐标为:(- ,
, )或(-
)或(- ,-
,- ).
).
故选D.
点评:本题考查了勾股定理,坐标与图形性质,相似三角形对应边成比例的性质,求出点C的横坐标与纵坐标的长度是解题的关键,作出图形更形象直观.
分析:利用勾股定理列式求出AB的长,再过点C作CD⊥AB于D,利用△ACD和△ABC相似,利用相似三角形对应边成比例列式求出AD、CD的长,再分点C在第二象限和第三象限两种情况讨论求解即可.
解答:
 解:如图,∵AC=3,BC=4,∠C=90°,
解:如图,∵AC=3,BC=4,∠C=90°,∴AB=
 =
= =5,
=5,过点C作CD⊥AB于D,
则△ACD∽△ABC,
∴
 =
= =
= ,
,即
 =
=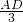 =
= ,
,解得CD=
 ,AD=
,AD= ,
,当点C在第二象限时,点C的坐标为(-
 ,
, ),
),当点C在第三象限时,点C的坐标为(-
 ,-
,- ),
),综上所述,点C的坐标为:(-
 ,
, )或(-
)或(- ,-
,- ).
).故选D.
点评:本题考查了勾股定理,坐标与图形性质,相似三角形对应边成比例的性质,求出点C的横坐标与纵坐标的长度是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.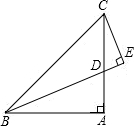 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.