题目内容
如图,AB是⊙O的直径,弦DC与AB相交于点E,若∠ACD=60°,∠ADC=50°,则∠ABD= °,∠CEB= °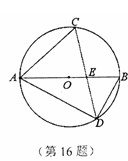

ABD=60°,∠CEB=100°
1)欲求∠ABD,已知了同弧所对的圆周角∠ACB的度数,根据同弧所对的圆周角相等即可得解;
(2)由于∠CEB是△ACE的外角,已知∠ACD的度数,欲求∠CEB,需先求出∠CAB的度数;可连接BC,由圆周角定理知∠ACB是直角,则∠A和∠CBA(即∠ADC)互余,由此得解.
解:(1)∵∠ABD、∠ACD是同弧所对的圆周角,

∴∠ABD=∠ACD=60°;
(2)连接BC,则∠ACB=90°;
∵∠CBA=∠ADC=50°,
∴∠CAB=90°-∠CBA=40°;
∴∠CEB=∠CAB+∠ACD=60°+40°=100°.
(2)由于∠CEB是△ACE的外角,已知∠ACD的度数,欲求∠CEB,需先求出∠CAB的度数;可连接BC,由圆周角定理知∠ACB是直角,则∠A和∠CBA(即∠ADC)互余,由此得解.
解:(1)∵∠ABD、∠ACD是同弧所对的圆周角,

∴∠ABD=∠ACD=60°;
(2)连接BC,则∠ACB=90°;
∵∠CBA=∠ADC=50°,
∴∠CAB=90°-∠CBA=40°;
∴∠CEB=∠CAB+∠ACD=60°+40°=100°.

练习册系列答案
相关题目

 B.
B.  c.2
c.2 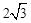 ,则扇形OCED的面积等于( ).
,则扇形OCED的面积等于( ).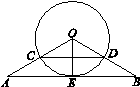
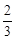 π B.
π B.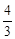 π C.
π C.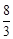 π D.
π D.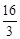 π
π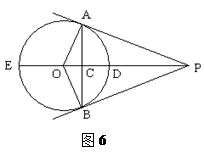
 与
与 是否相等?说明理由;
是否相等?说明理由;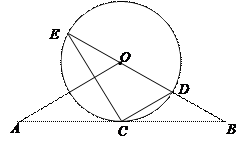
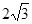 ,则点P到弦AB的距离为_____
,则点P到弦AB的距离为_____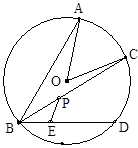
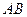 为
为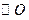 的直径,
的直径,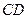 为弦,且
为弦,且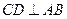 ,垂足为
,垂足为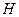 .
.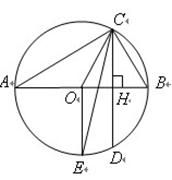
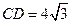 ,求
,求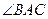 的度数;
的度数;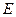 为
为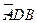 的中点,连结
的中点,连结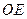 ,
,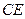 .求证:
.求证: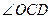 ;
;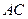 距离为3的点有多少个?并说明理由.
距离为3的点有多少个?并说明理由.