题目内容
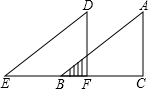如图所示，已知△ABC中，∠C=90°，BC=4厘米，AC=3厘米，△DEF与△ABC完全重合，当△ABC固定不变时，将△DEF沿CB所在的直线向左以1厘米/秒的速度移动________秒后，两个三角形重叠部分的面积为
平方厘米．
3
分析：根据图形证明重合部分的三角形与△ABC相似，再根据相似三角形的面积比等于相似比的平方，可求得BF的长，即可求得时间．
解答：设经过x秒后两个三角形重叠部分的面积为平方厘米，则BF=x，重合部分的三角形与△ABC相似，相似比是
，因而面积的比是：x2：16，△ABC的面积是
×4×3=6．得到：6=
，解得x=1．
所以CF=3，则移动的时间是3秒．
故答案是：3．
点评：本题考查对相似三角形性质的理解，相似三角形面积的比等于相似比的平方．
分析：根据图形证明重合部分的三角形与△ABC相似，再根据相似三角形的面积比等于相似比的平方，可求得BF的长，即可求得时间．
解答：设经过x秒后两个三角形重叠部分的面积为
平方厘米，则BF=x，重合部分的三角形与△ABC相似，相似比是，因而面积的比是：x2：16，△ABC的面积是×4×3=6．得到：6=，解得x=1．所以CF=3，则移动的时间是3秒．
故答案是：3．
点评：本题考查对相似三角形性质的理解，相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
如图所示，已知AB∥EF∥CD，若AB=6厘米，CD=9厘米．求EF．
5、如图所示，已知AB∥CD，EF平分∠CEG，∠1=80°，则∠2的度数为（ ）
如图所示，已知AB为圆O的直径，AC为弦，OD∥BC交AC于D，OD=2cm，求BC的长．
如图所示，已知AB=AC，BD⊥AC，试说明∠BAC=2∠CBD．