题目内容
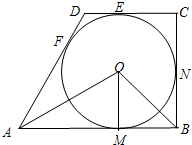 如图,梯形ABCD,AB∥CD,AB=2cm,梯形ABCD内部的⊙O分别切四边于E,F,M,N,且∠OAB=30°,∠OBA=45°.
如图,梯形ABCD,AB∥CD,AB=2cm,梯形ABCD内部的⊙O分别切四边于E,F,M,N,且∠OAB=30°,∠OBA=45°.
(1)求出⊙O的半径OM的长度;
(2)求出梯形ABCD的周长.
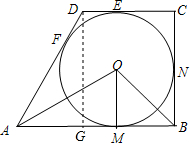 解:(1)∵⊙O切AB于M,
解:(1)∵⊙O切AB于M,∴OM⊥AB,
又∵∠OAB=30°,∠OBA=45°,
∴AM=
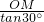 =
= OM,BM=
OM,BM=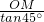 =OM,
=OM,∵AM+BM=AB,
∴
 OM+OM=2,
OM+OM=2,解得:OM=
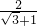 =
= -1;
-1;(2)过点D作DG⊥AB于点G,
∵⊙O分别切AB,AD于F,M,且∠OAB=30°,
∴∠DAB=60°,
又∵OM=
 -1,
-1,∴DG=BC=2(
 ),
),∴AD=
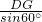 =2(
=2( )•
)• =
=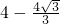 ,
,∴AG=
 AD=
AD=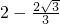 ,
,∴梯形ABCD的周长为:C梯形ABCD=2AB-AG+AD+BC=
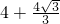 .
.分析:(1)由⊙O切AB于M,根据切线的性质,可得OM⊥AB,又由∠OAB=30°,∠OBA=45°,由三角函数的性质,可得AM=
 OM,BM=OM,继而可得
OM,BM=OM,继而可得 OM+OM=2,则可求得⊙O的半径OM的长度;
OM+OM=2,则可求得⊙O的半径OM的长度;(2)首先过点D作DG⊥AB于点G,由⊙O分别切AB,AD于F,M,且∠OAB=30°,根据切线长定理,即可求得∠BAD的度数,求得DG与BC的长,继而求得AD与AG的长,则可求得答案.
点评:此题考查了切线的性质、切线长定理以及三角函数的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 如图,梯形ABCD中,AB∥CD,E是AD中点,EF∥CB交AB于F,BC=4cm,则EF的长等于( )
如图,梯形ABCD中,AB∥CD,E是AD中点,EF∥CB交AB于F,BC=4cm,则EF的长等于( )| A、1.5cm | B、2cm | C、2.5cm | D、3cm |
 如图,梯形ABCD中,EF∥BC,AD=4,EF=5,BC=7,则DF:FC=
如图,梯形ABCD中,EF∥BC,AD=4,EF=5,BC=7,则DF:FC=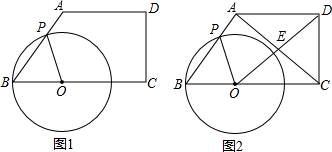
 如图,梯形ABCD内接于⊙O,AD∥BC,∠DAB=49°,则∠AOC的度数为
如图,梯形ABCD内接于⊙O,AD∥BC,∠DAB=49°,则∠AOC的度数为 如图,梯形ABCD中,DE∥AB交下底BC于E,AF∥CD交下底BC于F,且DE⊥AF,垂足为O.若AO=3cm,DO=4cm,四边形ABED的面积为36cm2,则梯形ABCD的周长为( )
如图,梯形ABCD中,DE∥AB交下底BC于E,AF∥CD交下底BC于F,且DE⊥AF,垂足为O.若AO=3cm,DO=4cm,四边形ABED的面积为36cm2,则梯形ABCD的周长为( )