题目内容
【例3】 设函数f(x)= ![]() -ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
-ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
解:任取x1、x2∈[0,+∞)且x1<x2,则
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
= -a(x1-x2)
-a(x1-x2)
=(x1-x2)(![]() -a).
-a).
(1)当a≥1时,∵![]() <1,
<1,
又∵x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴a≥1时,函数f(x)在区间[0,+∞)上为减函数.
(2)当0<a<1时,在区间[0,+∞)上存在x1=0,x2=![]() ,满足f(x1)=f(x2)=1,
,满足f(x1)=f(x2)=1,
∴0<a<1时,f(x)在[0,+∞)上不是单调函数.
评注: ①判断单调性常规思路为定义法;②变形过程中![]() <1利用了
<1利用了![]() >|x1|≥x1,
>|x1|≥x1, ![]() >x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
>x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
三、反函数的理解及应用
【例4】 设函数f(x)=![]() ,已知函数y=g(x)的图象与y=f--1(x+1)的图象关于直线y=x对称,求g(3)的值.
,已知函数y=g(x)的图象与y=f--1(x+1)的图象关于直线y=x对称,求g(3)的值.
分析一:f(x)→f-1(x)→f-1(x+1)→g(x)→g(3).
解法一:由y=f(x)= ![]() ,得f--1(x)=
,得f--1(x)= ![]() ,
,

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
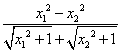 -a(x1-x2)
-a(x1-x2)