ЬтФПФкШн
ЁОЬтФПЁПвбжЊЃКдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() ЃЈ
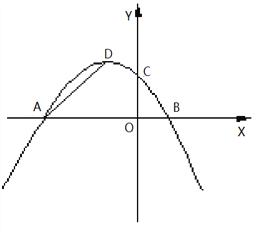
ЃЈ![]() ЃЉНЛxжсгкAЁЂBСНЕуЃЌНЛyжсгкЕуCЃЌЧвЖдГЦжсЮЊжБЯпx=ЈD2 .
ЃЉНЛxжсгкAЁЂBСНЕуЃЌНЛyжсгкЕуCЃЌЧвЖдГЦжсЮЊжБЯпx=ЈD2 .
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНМАЖЅЕуDЕФзјБъЃЛ
ЃЈ2ЃЉШєЕуP(0,t)ЪЧyжсЩЯЕФвЛИіЖЏЕуЃЌЧыНјааШчЯТЬНОПЃК
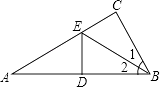
ЬНОПвЛЃКШчЭМ1ЃЌЩшЁїPADЕФУцЛ§ЮЊSЃЌСюWЃНtЁЄSЃЌЕБ0ЃМtЃМ4ЪБЃЌWЪЧЗёгазюДѓжЕЃПШчЙћгаЃЌЧѓГіWЕФзюДѓжЕКЭДЫЪБtЕФжЕЃЛШчЙћУЛгаЃЌЫЕУїРэгЩЃЛ
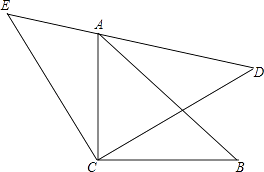
ЬНОПЖўЃКШчЭМ2ЃЌЪЧЗёДцдквдPЁЂAЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыRtЁїAOCЯрЫЦЃПШчЙћДцдкЃЌЧѓЕуPЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЭМ1 ЭМ2
ЁОД№АИЁПЃЈ1ЃЉyЃН![]() x2x+3ЃЎDЃЈ-2ЃЌ4ЃЉЃЎЃЈ2ЃЉЂйЕБt=3ЪБЃЌWгазюДѓжЕЃЌWзюДѓжЕ=18ЃЎЂкДцдкЃЎжЛДцдквЛЕуPЃЈ0ЃЌ2ЃЉЪЙRtЁїADPгыRtЁїAOCЯрЫЦЃЎ
x2x+3ЃЎDЃЈ-2ЃЌ4ЃЉЃЎЃЈ2ЃЉЂйЕБt=3ЪБЃЌWгазюДѓжЕЃЌWзюДѓжЕ=18ЃЎЂкДцдкЃЎжЛДцдквЛЕуPЃЈ0ЃЌ2ЃЉЪЙRtЁїADPгыRtЁїAOCЯрЫЦЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉЖдГЦжсЪЧжБЯпx=![]() ЃЌЧввбжЊХзЮяЯп
ЃЌЧввбжЊХзЮяЯп![]() ЃЈ
ЃЈ![]() ЃЉЕФЖдГЦжсЮЊжБЯпx=ЈD2ЃЌЙЪ
ЃЉЕФЖдГЦжсЮЊжБЯпx=ЈD2ЃЌЙЪ![]() ЃЌПЩЧѓГі aЕФжЕЃЌМДПЩаДГіХзЮяЯпЕФНтЮіЪНКЭЖЅЕузјБъЃЛЃЈ2ЃЉЬНОПвЛЃКгЩХзЮяЯп
ЃЌПЩЧѓГі aЕФжЕЃЌМДПЩаДГіХзЮяЯпЕФНтЮіЪНКЭЖЅЕузјБъЃЛЃЈ2ЃЉЬНОПвЛЃКгЩХзЮяЯп![]() ЕФНтЮіЪНПЩЧѓxЁЂyжсЕФНЛЕу
ЕФНтЮіЪНПЩЧѓxЁЂyжсЕФНЛЕу![]() ЕФзјБъЃЌзї
ЕФзјБъЃЌзї![]() жсгкMЃЌдђ
жсгкMЃЌдђ![]() ЃЌЕу
ЃЌЕу![]() ЃЌгЩ
ЃЌгЩ![]() ЃН
ЃН![]()
![]()
![]() ПЩЕУЃЌ
ПЩЕУЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌWгазюДѓжЕЃЌ
ЪБЃЌWгазюДѓжЕЃЌ![]() ЃЛЬНОПЖўЃКЗжШ§жжЧщПіЗжЮіЃКЂйЕБ
ЃЛЬНОПЖўЃКЗжШ§жжЧщПіЗжЮіЃКЂйЕБ![]() ЪБЃЌзї
ЪБЃЌзї![]() жсгкEЃЌдђ
жсгкEЃЌдђ![]() ЃЌдђ
ЃЌдђ![]() ЃЌдђ
ЃЌдђ![]() ЃЌдђ
ЃЌдђ![]() ЃЌгжвђЮЊ
ЃЌгжвђЮЊ![]() жсЃЌ
жсЃЌ![]() жсЃЌдђ
жсЃЌдђ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђДЫЪБга
ЃЌдђДЫЪБга ЃЌгжвђЮЊ
ЃЌгжвђЮЊ![]() ЃЌМД
ЃЌМД![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЃЌдђ
ЃЌдђ![]() ЃЌЫљвдЕБ
ЃЌЫљвдЕБ![]() ЪБЃЌДцдкЕуP1ЃЌЪЙ
ЪБЃЌДцдкЕуP1ЃЌЪЙ![]() ЃЌДЫЪБP1ЕуЕФзјБъЮЊЃЈ0ЃЌ2ЃЉЃЛЂкЕБ
ЃЌДЫЪБP1ЕуЕФзјБъЮЊЃЈ0ЃЌ2ЃЉЃЛЂкЕБ![]() ЪБЃЌдђ
ЪБЃЌдђ![]() ЃЌдђ
ЃЌдђ![]() ЃЌдђ
ЃЌдђ![]() ЃЌгжвђЮЊ
ЃЌгжвђЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌЫљвд
ЃЌЫљвд![]() гы
гы![]() ВЛЯрЫЦЃЌДЫЪБЕуP2ВЛДцдкЃЛЂлЕБ
ВЛЯрЫЦЃЌДЫЪБЕуP2ВЛДцдкЃЛЂлЕБ![]() ЪБЃЌвдADЮЊжБОЖзїЃЌдђ
ЪБЃЌвдADЮЊжБОЖзїЃЌдђ![]() ЕФАыОЖ
ЕФАыОЖ![]() ЃЌдВаФO1ЕНyжсЕФОрРы
ЃЌдВаФO1ЕНyжсЕФОрРы![]() ЃЌвђЮЊ
ЃЌвђЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() гыyжсЯрРыЃЌВЛДцдкЕуP3ЃЌЪЙ
гыyжсЯрРыЃЌВЛДцдкЕуP3ЃЌЪЙ![]() ,
,
ЫљвдзлКЯПЩЕУЃЌжЛДцдквЛЕу![]() ЪЙ
ЪЙ![]() гы
гы![]() ЯрЫЦЁЃ
ЯрЫЦЁЃ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉЁпХзЮяЯп![]() ЕФЖдГЦжсЮЊжБЯп
ЕФЖдГЦжсЮЊжБЯп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЬНОПвЛЃКЕБ![]() ЪБЃЌWгазюДѓжЕЃЌ
ЪБЃЌWгазюДѓжЕЃЌ
ЁпХзЮяЯп![]() НЛxжсгкAЁЂBСНЕуЃЌНЛyжсгкЕуCЃЌ
НЛxжсгкAЁЂBСНЕуЃЌНЛyжсгкЕуCЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌзї
ЪБЃЌзї![]() жсгкMЃЌШчЭМЫљЪОЃК
жсгкMЃЌШчЭМЫљЪОЃК

дђ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]()
![]() ЃЌ
ЃЌ![]()
![]()
Ёр![]()
ЁрЕБ![]() ЪБЃЌWгазюДѓжЕЃЌ
ЪБЃЌWгазюДѓжЕЃЌ![]() ЃЌ
ЃЌ
ЬНОПЖўЃКДцдкЃЌЗжШ§жжЧщПіЃК
ЂйЕБ![]() ЪБЃЌзї
ЪБЃЌзї![]() жсгкEЃЌШчЭМЫљЪОЃК
жсгкEЃЌШчЭМЫљЪОЃК
дђ![]() ЃЌ
ЃЌ
Ёр![]()
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
Ёп![]() жсЃЌ
жсЃЌ![]() жсЃЌ
жсЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
Ёр![]() ЃЌЃЌ
ЃЌЃЌ
ДЫЪБ ЃЌгжвђЮЊ
ЃЌгжвђЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌДцдкЕуP1ЃЌЪЙ
ЪБЃЌДцдкЕуP1ЃЌЪЙ![]() ЃЌДЫЪБP1ЕуЕФзјБъЮЊЃЈ0ЃЌ2ЃЉЃЛ
ЃЌДЫЪБP1ЕуЕФзјБъЮЊЃЈ0ЃЌ2ЃЉЃЛ
ЂкЕБ![]() ЪБЃЌдђ
ЪБЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() гы
гы![]() ВЛЯрЫЦЃЌДЫЪБЕуP2ВЛДцдкЃЛ
ВЛЯрЫЦЃЌДЫЪБЕуP2ВЛДцдкЃЛ
ЂлЕБ![]() ЪБЃЌвдADЮЊжБОЖзїЃЌдђ
ЪБЃЌвдADЮЊжБОЖзїЃЌдђ![]() ЕФАыОЖ
ЕФАыОЖ![]() ЃЌдВаФO1ЕНyжсЕФОрРы
ЃЌдВаФO1ЕНyжсЕФОрРы![]() ЃЌЁп
ЃЌЁп![]() ЃЌ
ЃЌ
Ёр![]() гыyжсЯрРыЃЌВЛДцдкЕуP3ЃЌЪЙ
гыyжсЯрРыЃЌВЛДцдкЕуP3ЃЌЪЙ![]() ЃЌ
ЃЌ
ЁрзлЩЯЫљЪіЃЌжЛДцдквЛЕу![]() ЪЙ
ЪЙ![]() гы
гы![]() ЯрЫЦЁЃ
ЯрЫЦЁЃ

 ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ
ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ
аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
УћЪІжИЕМвЛОэЭЈЯЕСаД№АИЁОЬтФПЁПЬНЫїгыгІгУЃЎ
ЃЈ1ЃЉЯШЬюаДЯТБэЃЌЭЈЙ§ЙлВьКѓдкЛиД№ЮЪЬтЃК
ЂйБэИёжаx=ЃЛy=ЃЛ
ЂкДгБэИёжаЬНОПaгы ![]() ЕФЪ§ЮЛЕФЙцТЩЃЌВЂРћгУетИіЙцТЩНтОіЯТУцСНИіЮЪЬтЃК
ЕФЪ§ЮЛЕФЙцТЩЃЌВЂРћгУетИіЙцТЩНтОіЯТУцСНИіЮЪЬтЃК
вбжЊ ![]() =1.8ЃЌШє
=1.8ЃЌШє ![]() =180ЃЌдђa= ЃЎ
=180ЃЌдђa= ЃЎ
вбжЊ ![]() =5.036ЃЌ
=5.036ЃЌ ![]() =15.906ЃЌдђ
=15.906ЃЌдђ ![]() = ЃЎ
= ЃЎ
a | Ё | 0.0001 | 0.01 | 1 | 100 | 10000 | Ё |
| Ё | 0.01 | x | 1 | y | 100 | Ё |
ЃЈ2ЃЉдФЖСР§ЬтЃЌШЛКѓЛиД№ЮЪЬтЃЛ
Р§ЬтЃКЩшaЁЂbЪЧгаРэЪ§ЃЌЧвТњзуa+ ![]() b=3Љ2
b=3Љ2 ![]() ЃЌЧѓa+bЕФжЕЃЎ
ЃЌЧѓa+bЕФжЕЃЎ
НтЃКгЩЬтвтЕУЃЈaЉ3ЃЉ+ЃЈb+2ЃЉ ![]() =0ЃЌвђЮЊaЁЂbЖМЪЧгаРэЪ§ЃЌЫљвдaЉ3ЃЌb+2вВЪЧгаРэЪ§ЃЌгЩгк
=0ЃЌвђЮЊaЁЂbЖМЪЧгаРэЪ§ЃЌЫљвдaЉ3ЃЌb+2вВЪЧгаРэЪ§ЃЌгЩгк ![]() ЪЧЮоРэЪ§ЃЌЫљвдaЉ3=0ЃЌb+2=0ЃЌЫљвдa=3ЃЌb=Љ2ЃЌЫљвдa+b=3+ЃЈЉ2ЃЉ=Љ1ЃЎ
ЪЧЮоРэЪ§ЃЌЫљвдaЉ3=0ЃЌb+2=0ЃЌЫљвдa=3ЃЌb=Љ2ЃЌЫљвдa+b=3+ЃЈЉ2ЃЉ=Љ1ЃЎ
ЮЪЬтЃКЩшxЁЂyЖМЪЧгаРэЪ§ЃЌЧвТњзуx2Љ2y+ ![]() y=10+3
y=10+3 ![]() ЃЌЧѓxyЕФжЕЃЎ
ЃЌЧѓxyЕФжЕЃЎ