题目内容
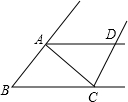
 如图,∠ABC=∠ABD﹢________,∠ECB=∠BCD-________.若EC是∠ACB的平分线,则∠BCE=________,∠DCE=
如图,∠ABC=∠ABD﹢________,∠ECB=∠BCD-________.若EC是∠ACB的平分线,则∠BCE=________,∠DCE= ________.
________.
∠DBC ∠DCE  ∠ACB ∠ACB
∠ACB ∠ACB
分析:根据角平分线的性质结合图形进行解答即可.
解答:由图可知,∠ABC=∠ABD﹢∠DBC,∠ECB=∠BCD-∠DCE.
∵EC是∠ACB的平分线,
∴∠BCE= ∠ACB,∠DCE=
∠ACB,∠DCE= ∠ACB.
∠ACB.
故答案为:∠DBC,∠DCE, ∠ACB,∠ACB.
∠ACB,∠ACB.
点评:本题考查的是角平分线的性质,熟知三角形的角平分线把一个角分为相等的两个角是解答此题的关键.
 ∠ACB ∠ACB
∠ACB ∠ACB分析:根据角平分线的性质结合图形进行解答即可.
解答:由图可知,∠ABC=∠ABD﹢∠DBC,∠ECB=∠BCD-∠DCE.
∵EC是∠ACB的平分线,
∴∠BCE=
 ∠ACB,∠DCE=
∠ACB,∠DCE= ∠ACB.
∠ACB.故答案为:∠DBC,∠DCE,
 ∠ACB,∠ACB.
∠ACB,∠ACB.点评:本题考查的是角平分线的性质,熟知三角形的角平分线把一个角分为相等的两个角是解答此题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
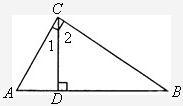
 ,且CB=CE.
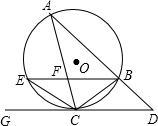
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.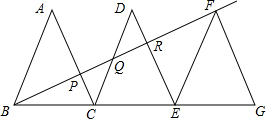 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且