题目内容
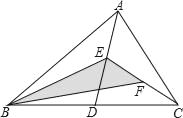
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 是边
是边![]() 中点,点
中点,点![]() 在边
在边![]() 上,且
上,且![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 的面积是________.
的面积是________.

【答案】![]()
【解析】
过点G作GM⊥AD于M,如图,先证明△ABE∽△DEF,利用相似三角形的性质计算出DF=![]() ,再利用正方形的性质判断△DGM为等腰直角三角形得到DM=MG,设DM=x,则MG=x,EM=1-x,然后证明△EMG∽△EDF,再利用相似三角形的性质计算出GM,再利用三角形面积公式计算S△DEG即可.
,再利用正方形的性质判断△DGM为等腰直角三角形得到DM=MG,设DM=x,则MG=x,EM=1-x,然后证明△EMG∽△EDF,再利用相似三角形的性质计算出GM,再利用三角形面积公式计算S△DEG即可.
过点G作GM⊥AD于M,如图,

∵FE⊥BE,
∴∠AEB+∠DEF=90°,
而∠AEB+∠ABE=90°,
∴∠ABE=∠DEF,
而∠A=∠EDF,
∴△ABE∽△DEF,
∴AB:DE=AE:DF,即2:1=1:DF,
∴DF=![]() ,
,
∵四边形ABCD为正方形,
∴∠ADB=45°,
∴△DGM为等腰直角三角形,
∴DM=MG,
设DM=x,则MG=x,EM=1-x,
∵MG∥DF,
∴△EMG∽△EDF,
∴MG:DF=EM:ED,即x:![]() =(1-x):1,解得x=
=(1-x):1,解得x=![]() ,
,
∴DM= MG=![]() ,
,
∴S△DEG=![]() ED·MG=
ED·MG=![]() ×1×
×1×![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目