题目内容
如图，在直角梯形ABCD中，已知AD∥BC，AB=BC，∠ABC=90°，DE=3cm，EC=4cm，DC=5cm，那么这个梯形ABCD的面积是
- A.
cm2 - B.
cm2 - C.12cm2
- D.13cm2
A
分析：根据勾股定理的逆定理判断△DCE是直角三角形，从而可以证明△ADE∽△BEC，设AE=x，进而根据相似三角形对应边的比相等分别表示BE、BC、AD的长，根据勾股定理求得x的值，进而求得梯形的面积．
解答：∵DE=3cm，EC=4cm，DC=5cm，
∴∠DEC=90°，
又∠ABC=90°，
∴∠AED=∠BCE，
∴△ADE∽△BEC．
设AE=x，则BC=
x，BE=
x，AD=
x，
在直角三角形BCE中，根据勾股定理，得
+
=16，
解得x2=
，
则这个梯形ABCD的面积是
×（
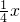+x）•x=（cm2）．
故选A．
点评：此题综合运用了勾股定理及其逆定理、相似三角形的判定和性质以及梯形的面积公式．
分析：根据勾股定理的逆定理判断△DCE是直角三角形，从而可以证明△ADE∽△BEC，设AE=x，进而根据相似三角形对应边的比相等分别表示BE、BC、AD的长，根据勾股定理求得x的值，进而求得梯形的面积．
解答：∵DE=3cm，EC=4cm，DC=5cm，
∴∠DEC=90°，
又∠ABC=90°，
∴∠AED=∠BCE，
∴△ADE∽△BEC．
设AE=x，则BC=
x，BE=x，AD=x，在直角三角形BCE中，根据勾股定理，得
+=16，解得x2=
，则这个梯形ABCD的面积是
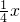×（+x）•x=（cm2）．故选A．
点评：此题综合运用了勾股定理及其逆定理、相似三角形的判定和性质以及梯形的面积公式．
练习册系列答案
相关题目
20、如图，在直角梯形ABCD中，AD∥BC，CD⊥BC，E为BC边上的点．将直角梯形ABCD沿对角线BD折叠，使△ABD与△EBD重合（如图中阴影所示）．若∠A=130°，AB=4cm，则梯形ABCD的高CD≈
如图，在直角梯形ABCD中，AB∥DC，∠D=90°，AC⊥BC，AB=10cm，BC=6cm，F点以2cm/秒的速度在线段AB上由A向B匀速运动，E点同时以1cm/秒的速度在线段BC上由B向C匀速运动，设运动时间为t秒（0＜t＜5）．
（1998•大连）如图，在直角梯形ABCD中．AD∥BC，DC⊥BC，且BC=3AD．以梯形的高AE为直径的⊙O交AB于点F，交CD于点G、H．过点F引⊙O的切线交BC于点N．
BC上的动点，点G在AB上，且四边形AEFG是矩形．设FG=x，矩形AEFG的面积为y．