题目内容
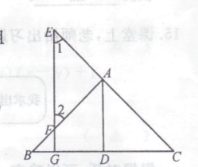
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1 , 得∠A1;∠A1BC和∠A1CD的平分线交于点A2 , 得∠A2;…∠A2016BC和∠A20l6CD的平分线交于点A2017 , 则∠A2017=°. 
【答案】![]()
【解析】解:∵A1B平分∠ABC,A1C平分∠ACD, ∴∠A1BC= ![]() ∠ABC,∠A1CA=
∠ABC,∠A1CA= ![]() ∠ACD,
∠ACD,
∵∠A1CD=∠A1+∠A1BC,
即 ![]() ∠ACD=∠A1+
∠ACD=∠A1+ ![]() ∠ABC,
∠ABC,
∴∠A1= ![]() (∠ACD﹣∠ABC),
(∠ACD﹣∠ABC),
∵∠A+∠ABC=∠ACD,
∴∠A=∠ACD﹣∠ABC,
∴∠A1= ![]() ∠A,
∠A,
∠A2= ![]() ∠A1=
∠A1= ![]() ∠A,…,
∠A,…,
以此类推可知∠A2017= ![]() ∠A=(
∠A=( ![]() )°,
)°,
故答案为: ![]() .
.
利用角平分线的性质、三角形外角性质,易证∠A1= ![]() ∠A,进而可求∠A1 , 由于∠A1=
∠A,进而可求∠A1 , 由于∠A1= ![]() ∠A,∠A2=
∠A,∠A2= ![]() ∠A1=
∠A1= ![]() ∠A,…,以此类推可知∠A2017即可求得.
∠A,…,以此类推可知∠A2017即可求得.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目