Question

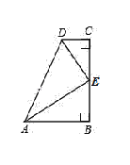
【题目】如图，△ABC和△CDE是以C为公共顶点的两个等腰三角形，且AC=CB，CD=CE，连接BD、AE相交于点M，连接CM，∠CAB=∠CDE=50°，则∠BMC=（ ）

A. 30°B. 40°C. 50°D. 60°

Answer 1

【答案】C

【解析】

首先证明△ACE≌△BCD，推出∠CAE=∠CBD，再利用“8字型”证明∠BMC=∠BAO=50°即可；

设AC交BM于点O．

∵AC=CB，CD=CE，∠CAB=∠CDE=50°，

∴∠CAB=∠CBA=∠CDE=∠CED=50°，

∴∠ACB=∠ECD=80°，

∴∠ACE=∠BCD，

在△AEC与△BDC中，

∴△ACE≌△BCD，

∴∠CAE=∠CBD，

∵∠AOM=∠BOC，

∴∠BMC=∠BAO=50°，

故选C