题目内容
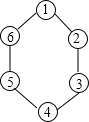 如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上,第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2003次跳2003步就跳到了________号位置上.
如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上,第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2003次跳2003步就跳到了________号位置上.
1
分析:棋子的跳法是有规律的,第一次跳1,第二次跳2,第三次跳3,…第N次跳N,则跳第N次后,棋子跳过的路程公式为:S=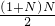 ,棋子一个周期为6,设K=
,棋子一个周期为6,设K=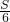 ,用K即可知道最后棋子的落位,若K为整数,则棋子落在1位;若K余1,则落2位,余2则落3位,余3则落4位,余4则落5位,余5则落6位.
,用K即可知道最后棋子的落位,若K为整数,则棋子落在1位;若K余1,则落2位,余2则落3位,余3则落4位,余4则落5位,余5则落6位.
解答:S=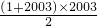 =2007006,
=2007006,
2007006÷6=334501,
所以应落在1号位.
故答案为:1.
点评:考查图形的规律性变化;根据棋子跳的总路程得到落脚处是解决本题的难点.
分析:棋子的跳法是有规律的,第一次跳1,第二次跳2,第三次跳3,…第N次跳N,则跳第N次后,棋子跳过的路程公式为:S=
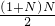 ,棋子一个周期为6,设K=
,棋子一个周期为6,设K=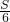 ,用K即可知道最后棋子的落位,若K为整数,则棋子落在1位;若K余1,则落2位,余2则落3位,余3则落4位,余4则落5位,余5则落6位.
,用K即可知道最后棋子的落位,若K为整数,则棋子落在1位;若K余1,则落2位,余2则落3位,余3则落4位,余4则落5位,余5则落6位.解答:S=
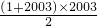 =2007006,
=2007006,2007006÷6=334501,
所以应落在1号位.
故答案为:1.
点评:考查图形的规律性变化;根据棋子跳的总路程得到落脚处是解决本题的难点.

练习册系列答案
相关题目
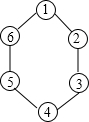 如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上,第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2003次跳2003步就跳到了
如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上,第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2003次跳2003步就跳到了