题目内容
直角三角形纸片的两直角边长分别为6，8，现将△ABC如图那样折叠，使点A与点B重合，折痕为DE，求BE的长．思路点拨：折叠之后，边AC被分成了两部分，其中AE折叠后变为图中的线段
BE
BE
，但BE与CE的和仍然是8，不妨设BE=x，则CE=8-x
8-x
，可以将问题转化到△ABC来解决．请你完成解题过程．）分析：根据翻折变换的性质得出BE=AE，设BE=x，则CE=8-x，在Rt△BCE中，由勾股定理：BC2+CE2=BE 2，求出x的值进而得出BE的长．
解答：解：设BE=x，AE=BE=x，则CE=8-x，
在Rt△BCE中，由勾股定理：BC2+CE2=BE 2，
即62+（8-x）2=x2，
解得：x=
，
即BE的长为
．
在Rt△BCE中，由勾股定理：BC2+CE2=BE 2，
即62+（8-x）2=x2，
解得：x=
| 25 |
| 4 |
即BE的长为
| 25 |
| 4 |
点评：此题主要考查了翻折变换的性质，利用翻折变换前后对应线段相等再由勾股定理得出是解题关键．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
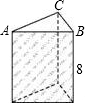如图，是一个直三棱柱的模型，其底面是两直角边长分别为3cm、4cm的直角三角形，侧棱长都是8cm．
如图，是一个直三棱柱的模型，其底面是两直角边长分别为3cm、4cm的直角三角形，侧棱长都是8cm．