题目内容
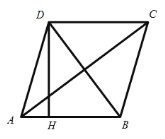
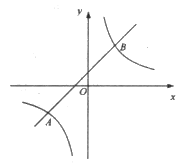
【题目】如图(1)A、E、F、C在同一直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC若AB=CD,G是EF的中点吗?请证明你的结论。若将 ⊿ABC的边EC经AC方向移动变为图(2)时,其余条件不变,上述结论还成立吗?为什么?

【答案】(1)G是EF的中点.(2)上述结论还成立,G是EF的中点.
【解析】
(1)连接BE、FD,首先由题意推出AF=CE,∠BFA=∠DEC=90°,则由全等三角形的判定定理HL证得Rt△BFA≌Rt△DEC,便知BF=DE,推出四边形BEDF为平行四边形,即可推出G是EF的中点;
(2)同(1)的证明过程.
解:(1)G是EF的中点.理由如下:
连接BE,DF,
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°.
又∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
∵AB=CD,
∴Rt△BFA≌Rt△DEC(HL),
∴BF=DE,
∵BF∥DE,
∴四边形BEDF为平行四边形,
∴EG=GF,
∴G是EF的中点.
(2)上述结论还成立.理由如下:
连接BE,DF,
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°.
又∵AE=CF,
∴AE-EF=CF-EF,即AF=CE,
∵AB=CD,
∴Rt△BFA≌Rt△DEC(HL),
∴BF=DE,
∵BF∥DE,
∴四边形BEDF为平行四边形,
∴EG=GF,
∴G是EF的中点.

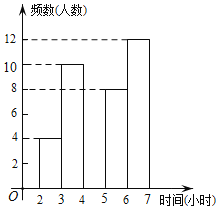
【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?