题目内容
方程|x-1|+|x-2|=3的解法要解方程|x-1|+|x-2|=3,就应设法化去绝对值符号,而要去掉绝对值符号就要判断x-1,x-2是正数还是负数?
解:令x-1=0得x=1,令x-2=0得x=2,分x<1、1≤x<2、x≥2三种情况化去绝对值符号.
当x<1时,原方程可化为(1-x)+(2-x)=3,
解得x=0.
当1≤x<2时,原方程可化为(x-1)+(2-x)=3,从而1=3,这不可能.说明x的值不可能是1≤x<2.
当x≥2时,原方程可化为x-1+x-2=3,解得x=3.
∴原方程的解为x=0和x=3.
读了上面的内容你有何启发?你能求方程|x+1|+|x+3|=5的解吗?试试看.
答案:
解析:
解析:
|
令x+1=0,得x=-1,令x+3=0得x=-3 分x<-3、-3≤x<-1、x≥-1三种情况化去绝对值符号. 当x<-3时,有-x-1-x-3=5,得x=-4 当-3≤x<-1时,有-x-1+x+3=5,无解; 当x≥-1时,有x+1+x+3=5,得x= 所以原方程的解为:x=-4 |

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
下列方程中,以x表示y的是( )
| A、x+y=8 | ||
B、x=
| ||
| C、2y=5x+7 | ||
| D、y=2x-1 |
关于x的分式方程
=
无解,则m的值为( )
| 2x |
| x+1 |
| m |
| x+1 |
| A、-2 | B、-1 | C、0 | D、2 |
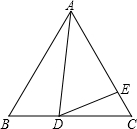 已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-
已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-