题目内容
(12分)如图,在平面直角坐标系中,已知点A(-2,-4),OB=2,抛物线y
=ax2+bx+c经过点A、O、B三点.
(1)求抛物线的函数表达式;
(2)若点M是抛物线对称轴上一点,试求AM+OM的最小值;
(3)在此抛物线上,是否存在点P,使得以点P与点O、A、B为顶点的四边形是梯形.若存在,求点P的坐标;若不存在,请说明理由.
:解:(1)由OB=2,可知B(2,0)
将A(-2,-4),B(2,0),O(0,0)三点坐标代入抛物线y=ax2+bx+c,得

解得:![]()
∴抛物线的函数表达式为![]() 。
。
(2)由![]() ,可得,抛物线的对称轴为直线
,可得,抛物线的对称轴为直线![]() ,且对称轴
,且对称轴![]() 是线段OB的垂直平分线,连结AB交直线
是线段OB的垂直平分线,连结AB交直线 于点M,即为所求。
于点M,即为所求。
∴MO=MB,则MO+MA=MA+MB=AB
作AC⊥x轴,垂足为C,则AC=4,BC=4,∴AB=![]()
∴MO+MA的最小值为![]() 。
。
(3)①若OB∥AP,此时点A与点P关于直线 对称,
对称,
由A(-2,-4),得P(4,-4),则得梯形OAPB。
②若OA∥BP,设直线OA的表达式为![]() ,由A(-2,-4)得,
,由A(-2,-4)得,![]() 。
。
设直线BP的表达式为![]() ,由B(2,0)得,
,由B(2,0)得,![]() ,即
,即![]() ,
,
∴直线BP的表达式为
由 ,解得
,解得![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
当![]() 时,
时,![]() ,∴点P(
,∴点P(![]() ),则得梯形OAPB。
),则得梯形OAPB。
③若AB∥OP,设直线AB的表达式为 ,则
,则
![]() ,解得
,解得![]() ,∴AB的表达式为
,∴AB的表达式为![]() 。
。
∴直线OP的表达式为![]() 。
。
由 ,得
,得 ![]() ,解得
,解得![]() ,(不合题意,舍去),此时点P不存在。
,(不合题意,舍去),此时点P不存在。
综上所述,存在两点P(4,-4)或P(![]() )使得以点P与点O、A、B为顶点的四边形是梯形。
)使得以点P与点O、A、B为顶点的四边形是梯形。
解析:略

练习册系列答案
相关题目
中国足球超级联赛2008-2009赛季共有16支球队参加比赛,30轮比赛后积分前10名球队的技术统计如表.请你根据表中提供的信息,解答下列问题:
(1)补全图(1)中的条形统计图;
(2)这十支球队在联赛中进球的平均数是 个(精确到个位);进球的中位数是 个;失球的众数是 个.
(3)进球数40个以上的球队战参赛球队的百分数为多少(精确到1%)?(未在表中的球队的进球数均少于40个)
(4)足球联赛负一场得0分,问胜一场、平一场分别得几分?
(1)补全图(1)中的条形统计图;
(2)这十支球队在联赛中进球的平均数是
(3)进球数40个以上的球队战参赛球队的百分数为多少(精确到1%)?(未在表中的球队的进球数均少于40个)
(4)足球联赛负一场得0分,问胜一场、平一场分别得几分?

| 名次 | 队名 | 胜 | 平 | 负 | 进球 | 失球 | 净胜球 | 积分 |
| 1 | 北京国安 | 20 | 07 | 03 | 57 | 28 | 29 | 67 |
| 2 | 天津康师傅 | 18 | 07 | 05 | 50 | 37 | 13 | 61 |
| 3 | 长春亚泰 | 18 | 05 | 07 | 54 | 42 | 8 | 59 |
| 4 | 上海申花 | 15 | 11 | 04 | 48 | 33 | 5 | 56 |
| 5 | 山东鲁能 | 15 | 11 | 04 | 52 | 31 | 21 | 56 |
| 6 | 浙江绿城 | 12 | 10 | 08 | 41 | 38 | 3 | 46 |
| 7 | 陕西中新 | 12 | 08 | 10 | 45 | 45 | 0 | 44 |
| 8 | 贵州医药 | 10 | 10 | 10 | 39 | 43 | -4 | 40 |
| 9 | 青岛中能 | 10 | 10 | 10 | 37 | 45 | -8 | 40 |
| 10 | 江苏舜天 | 08 | 15 | 07 | 37 | 45 | -8 | 39 |
中国足球超级联赛2008-2009赛季共有16支球队参加比赛,30轮比赛后积分前10名球队的技术统计如表.请你根据表中提供的信息,解答下列问题:
(1)补全图(1)中的条形统计图;
(2)这十支球队在联赛中进球的平均数是______个(精确到个位);进球的中位数是______个;失球的众数是______个.
(3)进球数40个以上的球队战参赛球队的百分数为多少(精确到1%)?(未在表中的球队的进球数均少于40个)
(4)足球联赛负一场得0分,问胜一场、平一场分别得几分?

(1)补全图(1)中的条形统计图;
(2)这十支球队在联赛中进球的平均数是______个(精确到个位);进球的中位数是______个;失球的众数是______个.
(3)进球数40个以上的球队战参赛球队的百分数为多少(精确到1%)?(未在表中的球队的进球数均少于40个)
(4)足球联赛负一场得0分,问胜一场、平一场分别得几分?
| 名次 | 队名 | 胜 | 平 | 负 | 进球 | 失球 | 净胜球 | 积分 |
| 1 | 北京国安 | 20 | 07 | 03 | 57 | 28 | 29 | 67 |
| 2 | 天津康师傅 | 18 | 07 | 05 | 50 | 37 | 13 | 61 |
| 3 | 长春亚泰 | 18 | 05 | 07 | 54 | 42 | 8 | 59 |
| 4 | 上海申花 | 15 | 11 | 04 | 48 | 33 | 5 | 56 |
| 5 | 山东鲁能 | 15 | 11 | 04 | 52 | 31 | 21 | 56 |
| 6 | 浙江绿城 | 12 | 10 | 08 | 41 | 38 | 3 | 46 |
| 7 | 陕西中新 | 12 | 08 | 10 | 45 | 45 | 0 | 44 |
| 8 | 贵州医药 | 10 | 10 | 10 | 39 | 43 | -4 | 40 |
| 9 | 青岛中能 | 10 | 10 | 10 | 37 | 45 | -8 | 40 |
| 10 | 江苏舜天 | 08 | 15 | 07 | 37 | 45 | -8 | 39 |


 、
、 两地之间架设高压电线,测量人员在相距
两地之间架设高压电线,测量人员在相距 、
、 两地(
两地( ,
, ,
, ,
, (如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是
(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是 倍,问施工单
倍,问施工单 )
)
 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么 的度数为 。
的度数为 。

 x2+bx+c经过B、P两点,求抛物线的解析式;
x2+bx+c经过B、P两点,求抛物线的解析式;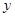 轴的平
轴的平