题目内容
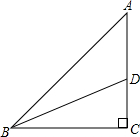（2012•仪征市一模）如图，在△ABC中，∠C=90，点D在AC上，将△BCD沿BD翻折，点C落在斜边AB上，DC=2，则点D到斜边AB的距离是2
2
．分析：过D作DE⊥AB于点E，根据翻折可得∠ABD=∠CBD，再根据角平分线上的点到角的两边的距离相等可得DE=DC，从而得解．
解答：
解：如图，过D作DE⊥AB于点E，
∵△BCD沿BD翻折，点C落在斜边AB上，
∴∠ABD=∠CBD，
又∵∠C=90，
∴DE=DC，
∵DC=2，
∴DE=2，
即点D到斜边AB的距离是2．
故答案为：2．
解：如图，过D作DE⊥AB于点E，∵△BCD沿BD翻折，点C落在斜边AB上，
∴∠ABD=∠CBD，
又∵∠C=90，
∴DE=DC，
∵DC=2，
∴DE=2，
即点D到斜边AB的距离是2．
故答案为：2．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，翻折变换的性质，判断出∠ABD=∠CBD并熟记角平分线的性质是解题的关键．
练习册系列答案
相关题目
（2012•仪征市一模）观察下列图形，则第n个图形中三角形的个数是